It is known that the time of revolution T of a satellite around the earth depends on the universal gravitational constant G, the mass of the earth M, and the radius of the circular orbit R. Obtain an expression for T using dimensional analysis.
We have [T]∝[G]a[M]b[R]c
⇒[M]a[L]0[T]1=[M]−a[L]3a[T]−2a×[M]b×[L]c=[M]b−a[L](c+3a)[T]−2a
Comparing the exponents
For [T]: 1=−2a⇒a=−12 For [M]: 0=b−a⇒b−a=−12
For [L]: 0=c+3a⇒c=−3a=32
Putting the values we get T∝G−1/2M−1/2R3/2⇒T∝√R3GM
The actual expression is T =2π√R3GM
Topper's Solved these Questions
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - BEGINNER S BOX-1
2 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - BEGINNER S BOX-2
4 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - SUBJECTIVE QUESTION
9 Videos
- SEMICONDUCTORSBOOK - ALLENCHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
51 Videos
Similar Questions
The speed v of a satellite moving in a circular orbit around the earth depends on the gravitational constant G, mass of the earth me and radius of circular orbit r. Estabish the relation using dimensions.
View SolutionA satellite revolves around the earth in a circular orbit. What will happen to its orbit if universal gravitational constant start decreasing with time.
View Solution
Knowledge Check
The escape velocity of a sphere of mass m is given by (G=Universal gravitational constant,M=Mass of the earth and Re=Radius of the earth)
A√2GMmReB√2GMReC√GMReD√2GMm+ReReA satellite is revolving round the earth. If the universal gravitational constant(G)was decreasing imiformly with time for the satellite, the quantity that still remains constant is
AWeightBRadiusCTangential speedDAngular momentumThe acceleration due to gravity'g' for objects on or near the surface of earth is related to the universal gravitational constant 'G' as ('M' is the mass of the earth and 'R' is its radius):
AG=g(M)R2Bg=GMR2CM=gGR2DR=gGM2
Obtain an expressing for critical velocity of a satellite orbiting around the earth.
View SolutionObtain an expression for the critical velocity of a satellite orbiting around the Earth.
View SolutionLength of a year on a planet is the duration in which it completes one revolution around the sun. Assume path of the planet known as orbit to be circular with sun at the centre. The length T of a year of a planet orbiting around the sun in circular orbit depends on universal gravitational constant G, mass ms of the sun and radius r of the orbit. if T∝Gambsrc find value of a+b+2c.
View SolutionMatch the Column I with Column II
For a satellite in circular orbit
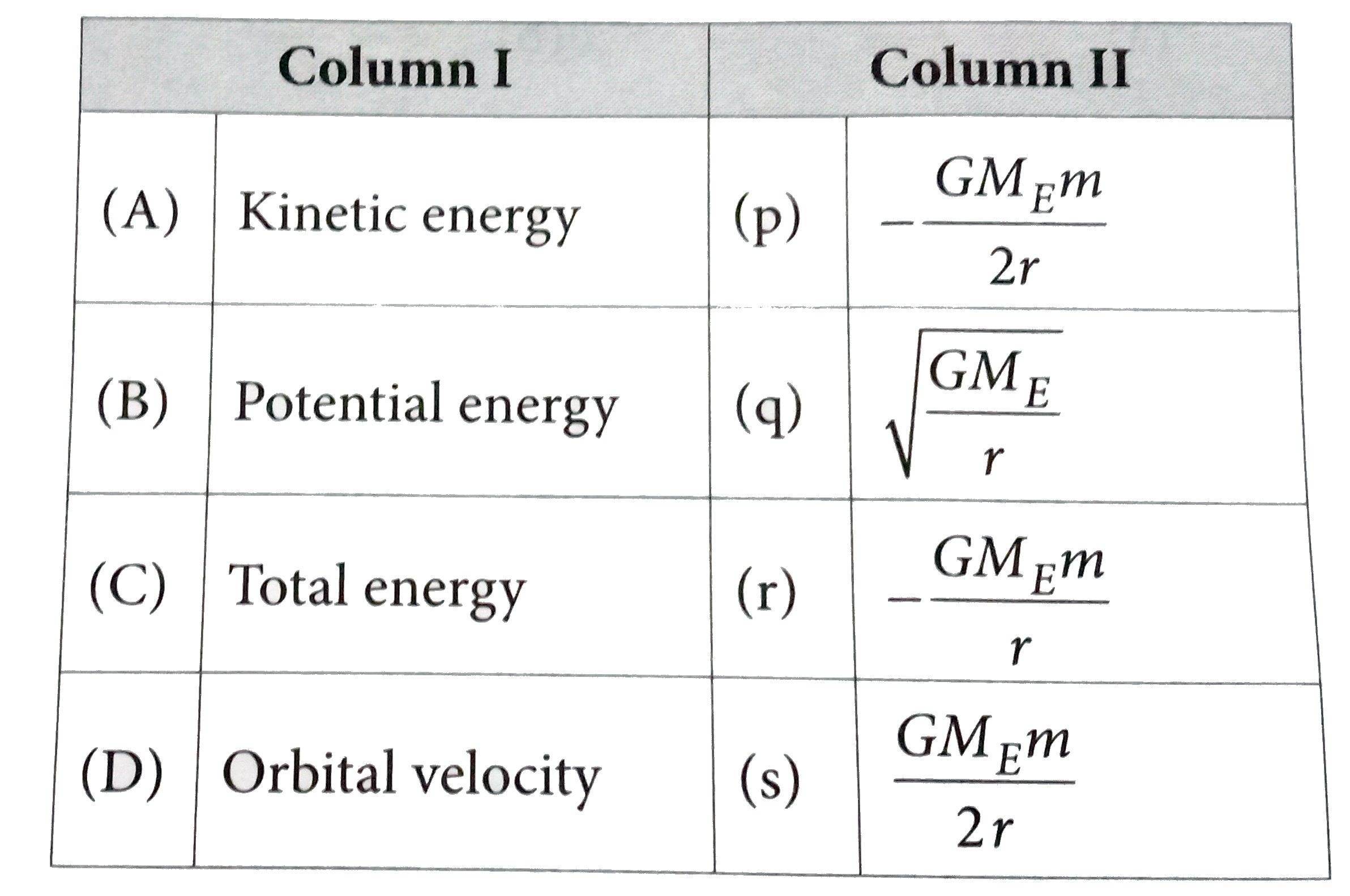
(where ME is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )
View SolutionIf a time period of revolution of a satellite around a planet in a circular orbit of radius r is T,then the period of revolution around planet in a circular orbit of radius 3r will be
View Solution
