Question

A particle of mass 2 kg moves on a circular path with constant speed 10 m$/$ s . Find change in speed and magnitude of change in velocity. Whan particle completes half revolution.

Explanation

To solve the problem step by step, let's break it down:

Step 1: Understand the Problem
We have a particle of mass 2 kg moving in a circular path with a constant speed of 10 m/s. We need to find the change in speed and the magnitude of the change in velocity when the particle completes half a revolution.

Step 2: Analyze Change in Speed
Since the particle is moving with a constant speed, the speed at any point during its motion remains the same. Therefore, the speed at the starting point (Point A) and the speed at the point after half a revolution (Point B) will both be 10 m/s.

- Speed at Point A (V1) = 10 m/s
- Speed at Point B (V2) = 10 m/s

Change in Speed:
\( \Delta \text{Speed} = V2 - V1 = 10 \, \text{m/s} - 10 \, \text{m/s} = 0 \, \text{m/s} \)

Step 3: Analyze Change in Velocity
Velocity is a vector quantity, which means it has both magnitude and direction. While the speed remains constant, the direction of the velocity changes as the particle moves along the circular path.

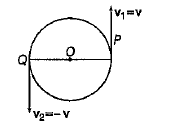
- At Point A, let's assume the velocity vector is directed along the positive x-axis:
\( \vec{V1} = 10 \hat{i} \, \text{m/s} \)

- After completing half a revolution, at Point B, the velocity vector will be directed along the negative x-axis:
\( \vec{V2} = -10 \hat{i} \, \text{m/s} \)

Change in Velocity:
\( \Delta \vec{V} = \vec{V2} - \vec{V1} = (-10 \hat{i}) - (10 \hat{i}) = -20 \hat{i} \, \text{m/s} \)

Step 4: Calculate Magnitude of Change in Velocity
The magnitude of the change in velocity is given by the absolute value of the change in velocity vector:
\( |\Delta \vec{V}| = |-20 \hat{i}| = 20 \, \text{m/s} \)

Final Answers
- Change in Speed: \(0 \, \text{m/s}\)
- Magnitude of Change in Velocity: \(20 \, \text{m/s}\)