A wheel of radius 'R' is placed on ground and its contact point 'P'. If wheel starts rolling without slipped and completes half a revolution, find the displacement of point.


Displacement = √(πR)2+(2R)2=R√π2+4
Topper's Solved these Questions
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-2
7 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-3
2 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Integer Type Question
3 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - SUBJECTIVE QUESTION
9 Videos
Similar Questions
A body is moving along the circumference of a circle of radius R and completes half of the revolution then the ratio of its displacement to distance is
View SolutionA wheel of circumference C is at rest on the ground. When the wheel rolls forward through half a revolution, then the displacement of initial point of contact will be
View Solution
Knowledge Check
A body is moving along the circumference of a circle of radius R and completes half of the revolution. Then the ratio of its displacement to distance is
Aπ:2B2:1C2:πD1:2A wheel of radius R rolls without slipping on a horizontal ground. The distance travelled by a point on the rim in one complete rotation is:
A2πRB8RC2RDπRThe radius of a wheel is R and its radius of gyration about its axis passing through its center and perpendicular to its plane is K. If the wheel is rolling without slipping the ratio of its rotational kinetic energy to its translational kinetic energy is-
AK2R2BR2K2CR2R2+K2DK2R2+K2
A ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.



View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
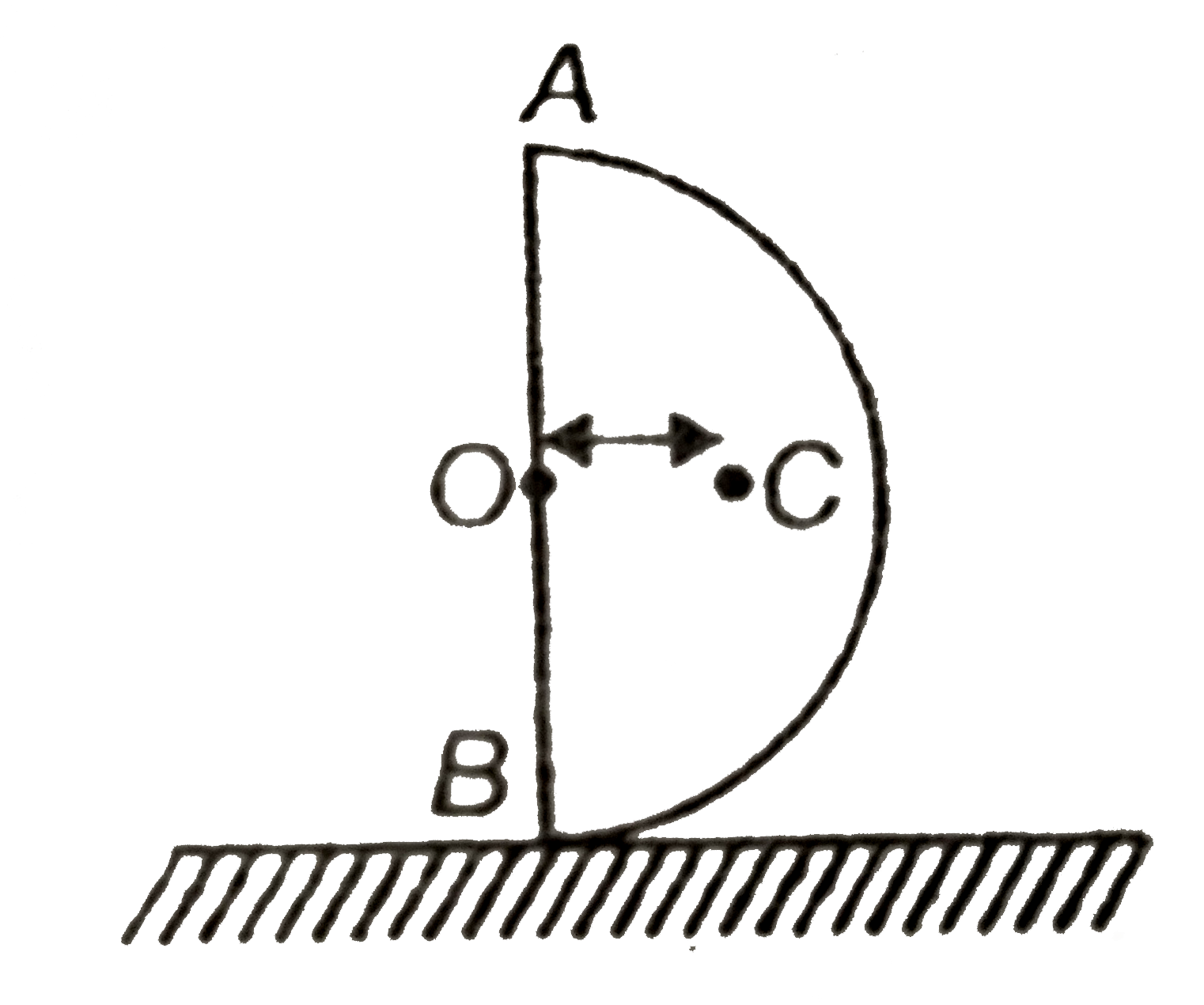
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
View SolutionDuring rolling without slipping, what is the velocity of the point in contact with the surface.
View SolutionA uniform sphere of mass m and radius R starts rolling without slipping down an inclined plane at an angle α to the horizontal. Find the time dependence of the angular momentum of the sphere relative to the point of contact at the initial moment. How will the obtained result change in the case of a perfectly smooth inclined plane?
View SolutionThe radius of a wheel is R and its radius of gyration about its axis passing through its center and perpendicualr to its plane is K. If the wheel is roling without slipping. Then the ratio of tis rotational kinetic energy to its translational kinetic energy is
View Solution
