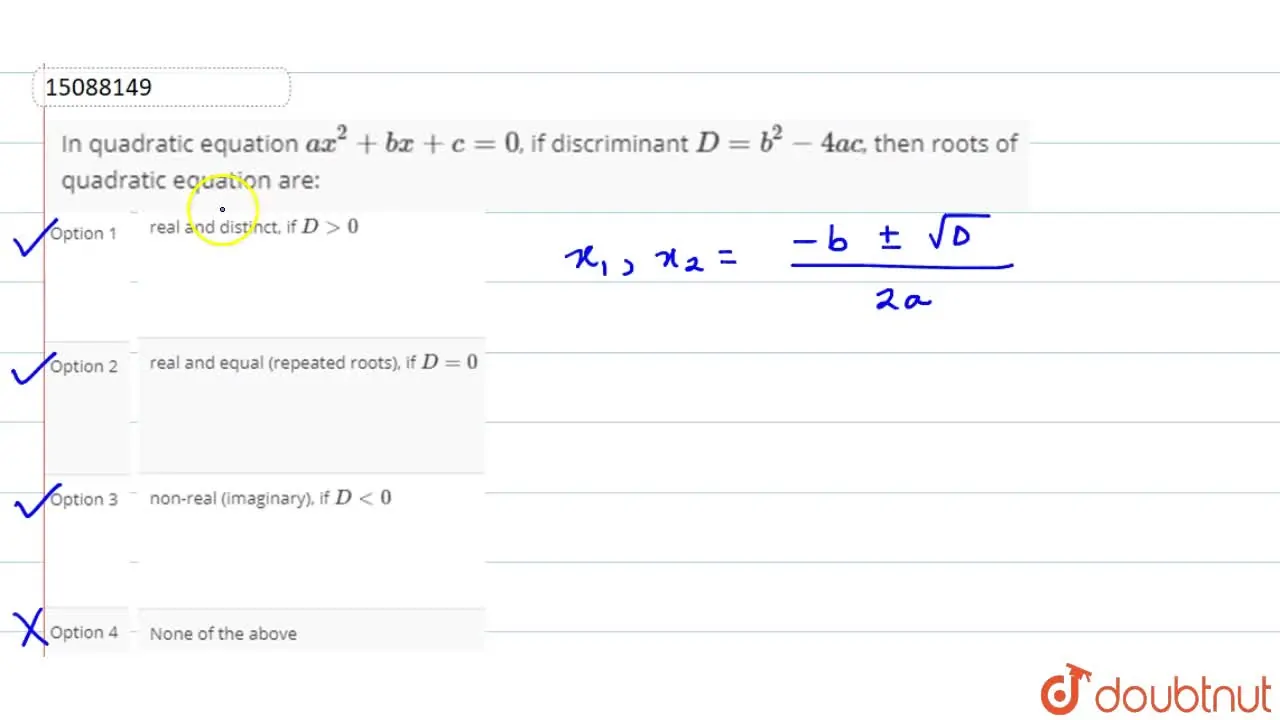
In quadratic equation $a x^{2} + b x + c = 0$ , if discriminant $D = b^{2} - 4 a c$ , then roots of quadratic equation are:

Real and distinct, if $D > 0$

Real and equal (i.e., repeated roots), if $D = 0$

Non-real (i.e., imaginary), if $D < 0$

All of the above are correct

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Answer

Step by step video, text & image solution for In quadratic equation ax^(2)+bx+c=0, if discriminant D=b^(2)-4ac, then roots of quadratic equation are: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS BASIC MATHEMATICS USED IN PHYSICS &VECTORS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A quadratic equation $a x^{2} + b x + c = 0$ may have
Atwo real roots
Btwo non-real roots
Cone real and one non-real root
DEither (a) or (b)
Question 2 - Select One
In the equation $a x^{2} + b x + c = 0$ , it is given that $D = (b^{2} - 4 a c) > 0 .$ Then, the roots of the equation are
Areal and equal
Breal and unequal
Cimaginary
DNone of these
Question 3 - Select One
Assertion (A) : The roots of the quadratic equation $x^{2} + 2 x + 2 = 0$ are imaginary.
Reason (R ) : If discriminant $D = b^{2} - 4 a c < 0$ then the roots of the quadratic equation $a x^{2} + b x + c = 0$ are imaginary.
ABoth A and R are true and R is the correct explanation for A.
BBoth A and R are true and R is not correct explanation for A.
CA is true but R is false
DA is false but R is true

ALLEN-BASIC MATHEMATICS USED IN PHYSICS &VECTORS -BEGINNER S BOX 6

Home
Ask Doubt
Profile

In quadratic equation ax2+bx+c=0, if discriminant D=b2−4ac, then roots of quadratic equation are:

The correct Answer is:D

Topper's Solved these Questions

Similar Questions

Knowledge Check

A quadratic equation ax2+bx+c=0 may have

In the equation ax2+bx+c=0, it is given that D=(b2−4ac)>0. Then, the roots of the equation are

Assertion (A) : The roots of the quadratic equation x2+2x+2=0 are imaginary. Reason (R ) : If discriminant D=b2−4ac<0 then the roots of the quadratic equation ax2+bx+c=0 are imaginary.

ALLEN-BASIC MATHEMATICS USED IN PHYSICS &VECTORS -BEGINNER S BOX 6

In quadratic equation $a x^{2} + b x + c = 0$ , if discriminant $D = b^{2} - 4 a c$ , then roots of quadratic equation are:

A quadratic equation $a x^{2} + b x + c = 0$ may have

In the equation $a x^{2} + b x + c = 0$ , it is given that $D = (b^{2} - 4 a c) > 0 .$ Then, the roots of the equation are

Assertion (A) : The roots of the quadratic equation $x^{2} + 2 x + 2 = 0$ are imaginary.
Reason (R ) : If discriminant $D = b^{2} - 4 a c < 0$ then the roots of the quadratic equation $a x^{2} + b x + c = 0$ are imaginary.