Match the following List I to List II

The correct Answer is:a→q;b→q;c⊤,r;dtop,s
a. Since angles A,B and C are acute angles, we have
A+B>π/2
A>π2−B
⇒sinA−cosB>0
⇒cosB−sinA<0...(i)
Again, B>π2−A
sinB>cosA
sinB−cosA>0…(ii)
From Eqs. (i) and (ii), we get that x-coordinate is -ve and y-coordinate is +ve.
therefore, point is in 2nd quadrant only.
b. 2sinθ>1⇒sinθ>0
⇒θ∈1stor 2nd quadrant
3cosθ<1⇒cosθ<0
⇒θ∈2ndor3rd quadrant
Hence,θ∈2nd quadrant
c. |cosx+sinx|=|sinx|+|cosx|
Thus, cosx and sinx must have same sign or at least one is zero.
d. L.H.S.=1−sinA|cosA|+sinAcosA=1cosA,
which is true only if |cosA|=cosA
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Numerical)
11 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - JEE Main Previous Year
2 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercise (Comprehension)
11 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Matrix Match Type)
1 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGECHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Videos
Similar Questions
Let x and y be positive real numbers such that y3+y≤x−x3 . Then match the following list -I with List- II Where [.] is greatest integer function.
List - I List - II(P)[x1x−y1y](1)−1(Q)[x1x−1](2) 0(R) [3−(1−x)2](3) 1(s) [x2−y2+1](4)2
View SolutionMatch the following itmes of List -I and List - II

View Solution
Knowledge Check
Match the following List -I and List - II
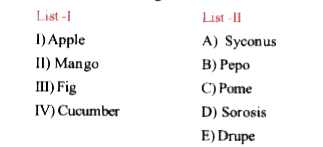 AI-E,II-C,IN-B.IV-DBI-A,II-E,III-B, IV-DCI-A,II-B,III-C, IV-DDI-C, II-E,III-A.IV-B
AI-E,II-C,IN-B.IV-DBI-A,II-E,III-B, IV-DCI-A,II-B,III-C, IV-DDI-C, II-E,III-A.IV-BMatch the following List-I with List-II.
 APQRS2413BPQRS3142CPQRS1324DPQRS2431
APQRS2413BPQRS3142CPQRS1324DPQRS2431Match the following List-I and List-II List-I A.
 AA-2, B-4, C-1, D-3BA-3, B-2, C-1, D-4CA-1, B-2, C-3, D-4DA-4, B-3, C-2, D-1
AA-2, B-4, C-1, D-3BA-3, B-2, C-1, D-4CA-1, B-2, C-3, D-4DA-4, B-3, C-2, D-1
Match the following in List-I with List II and select the corect option :-
List−IList−IIaKP=QiAlways nonspontaneousbT>ΔH/SiiIsothrmal processcΔH=+veΔS=veiiiEquilibriumdq=veivspontaneous and endothermic
View SolutionMatch the following
List IList IIA) HerbicideI) Oxidizing nature B) PhotochemicalII) Benzopyrene smog C) London smog III) NaClO3D) Carcinogenic substance iv) Reducing nature
The correct match is
View SolutionMatch the following
List I List IIA)Green house effectI) Over nutritionB)HNO3+H2SO4II) Water pollution D) Eutrophication IV) Air pollution
The correct match is
View SolutionMatch of the following List-I and List-II
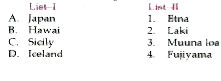
View SolutionMatch the following items of List -I and List - II

View Solution
