A sector OABO of central angle θ is constructed in a circle with centre O and of radius 6. The radius of the circle that is circumscribed about the triangle OAB, is 6cosθ2 (b) 6secθ2 3secθ2 (d) 3(cosθ2+2)
6cos.θ2
6sec.θ2
3sec.θ2
3(cos.θ2+2)
The correct Answer is:C
Let the required radius be R
∴R=abc4Δ,Δ=12.6.6.sinθ=18sinθ

and a=b=6
Now, sin.θ2=c12
⇒c=12sin.θ2
∴R=36.12sin(θ/2)4.18.sinθ=3sec.θ2
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Multiple)
24 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Comprehension)
34 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.11
4 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
32 Videos
Similar Questions
A sector OABO of central angle θ is constructed in a circle with centre O and of radius 6. The radius of the circle that is circumscribed about the triangle OAB, is 6cosθ2 (b) 6secθ2 3secθ2 (d) 3(cosθ2+2)
View SolutionThe intercept made by the circle with centre (2, 3) and radius 6 on y-axis is
View Solution
Knowledge Check
ABC is a right-angled triangle with AB = 6 cm and BC = 8 cm. A circle with centre O has been in scribed inside ΔABC. The radius of the circle is
A1 cmB2 cmC3 cmD4 cm
find the equation of circle whose centre (−3,−2) and radius 6
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
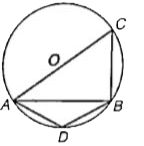
View SolutionIn the given diagram, 'O' is the centre of the circle and AC is the diameter. ∠ADB is 120∘. Radius of the circle is 6 cm, what is the area of the triangle ABC?
View SolutionPoints A(−1,y) and B(5,7) lie on a circle with centre O(2,−3y). Find the values of y. Hence, find the radius of the circle.
View SolutionPoints A(−1,y) and B(5,7) lie on a circle with centre O(2,−3y) . Find the values of y. Hence, find the radius of the circle.
View SolutionThe area of a minor sector of a circle is 3.85cm2 and the measure of its central angle is 36∘. Find the radius of the circle.
View SolutionABC is an equilateral triangle of side 6 cm, a circle, centre O, passes through the vertices A, B, and C. Find the radius of the circle.
View Solution
