Let ABC be an acute angled triangle whose orthocentre is at H. If altitude from A is produced to meet the circumcircle of triangle ABC at D , then prove HD=4RcosBcosC
Video Solution
Text Solution

In the figure, altitude AD meets BC at D and circumcircle at P. In circumcircle of triangle ABC, chord AB subtends same angle at point C and P.
∴Ang≤BPA=∠BCA=C
i.e., ∠BPD=C
Also ∠HBD=90∘−C∴∠BHD=C
Thus ΔBPDandΔBHD are similar.
∴HD=DP
Therefore, P is image of H in BC
Also, HP=2HD=2(2RcosBcosC)
=4RcosBcosC
|
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.1
Explore 12 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.2
Explore 8 Videos
- PROGRESSION AND SERIESBook:CENGAGEChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBook:CENGAGEChapter:PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEExercise:Question Bank
Explore 32 Videos
Similar Questions
Knowledge Check
In an acute-angled triangle ABC, tanA+tanB+tanC
A≥3B≥√3C≥3√3Dnone of theseIf AD, BE, CF are the altitudes of ΔABC whose orthocentre is H, then C is the orthocentre of :
A△ABHB△BDHC△ABDD△BEALet ABC be a triangle and O be its orthocentre .If R and R1 are the circum-radii of triangle ABC and AOB , then
AR1>RBR1=RCR1<RDnone of these
In given figure, ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
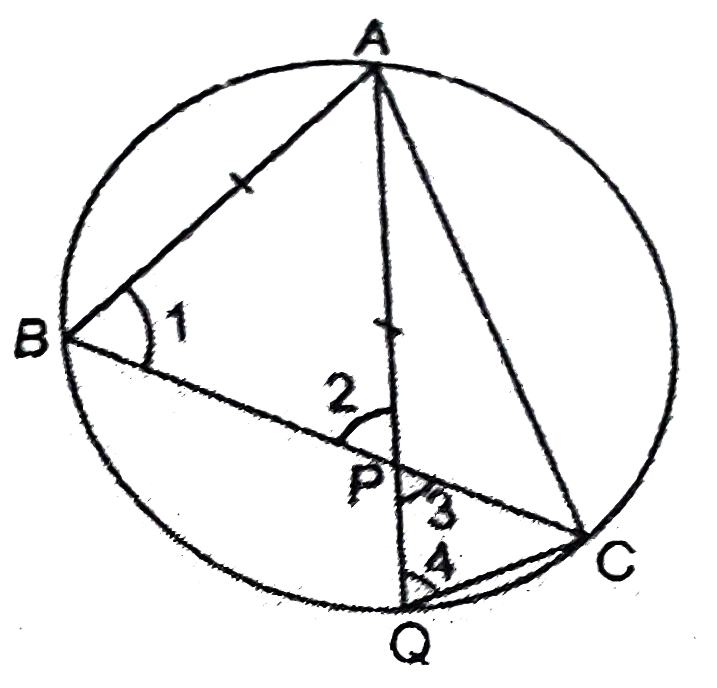
View SolutionABC is an acute angled triangle with circumcenter O and orthocentre H. If AO=AH, then find the angle A.
View SolutionIf AD, BE, CF are the altitudes of triangle ABC whose ortho centre is H then C is ortho centre of
View SolutionFind the lengths of chords of the circumcircle of triangle ABC, made by its altitudes
View SolutionLet ABC be an equilateral triangle with side length a. Let R and r denote the radii of the circumcircle and the incircle of triangle ABC respectively. Then, as a function of a, the ratio Rr
View Solution
