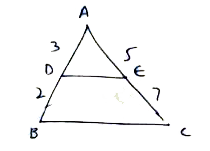
Each side of triangle ABC is divided into three equal parts. Find the ratio of the are of hexagon PQRSTU to the area of the triangle ABC.
Area of hexagon PQRSTU
Δ1= area of ΔABC− area of ΔAPQ− area of ΔBTU− area of ΔCRS
=Δ−12(b3.c3sinA)−12(a3.c3sinB)−12(a3.b3sinC)
=Δ−Δ3=2Δ3
∴Δ1Δ=23
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.1
12 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.2
8 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
32 Videos
Similar Questions
Knowledge Check
If D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
A1:4B1:2C1:3D2:3
In a triangle ABC, median BE and CF intersect at O. Find the ratio of area of ΔOFEandΔABC.
View SolutionThe product of the arithmetic mean of the lengths of the side of a triangle ABC and harmonic mean of the lengths of the altitudes of the triangle is equal to (Delta is area of triangle ABC).
View SolutionIn Fig. 9.29 ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of triangle ACD.
View SolutionThree straight lines are drawn through the three vertices of a triangle ABC, the line through each vertex being parallel to the opposite side. The triangle DEF is bounded by these parallel lines. Consider the following statements in respect of the triangle DEF :
1. Each side of triangle DEF is double the side of triangle ABC to which it is parallel.
2. Area of triangle DEF is four times the area of triangle ABC.
Which of the above statements is/are correct?
View SolutionPis a point inside the triangle ABC. Lines are drawn through P, parallel to the sides of the triangle.The three resulting triangles with the vertex at P have areas 4,9and49sq. units. The area of thetriangle ABC is -
View SolutionSides of triangle ABC, a, b, c are in G.P. If 'r' be the common ratio of this G.P. , then
View SolutionIn a triangle ABC with the right angle C, side BC is divided by points D and E into three equal parts. Find the sum of angles AEC, ADC, and ABC if it is known that BC=3AC
View Solution