In ABC, as semicircle is inscribed, which lies on the side ⋅ If x is the lengthof the angle bisector through angle C, then prove that the radius of the semicircle is xsin(C2).

From the figure
(12)ra+(12)rb=(12)absinC
or r(a+b)=2Δ
or r=2Δa+b=absinCa+b
Also x=2aba+bcos.C2 [length of angle bisector]
From Eq. (i), r=2×(1/2)absinCa+b
=2absin.C2cos.C2a+b
=2abcos.C2a+bsin.C2
=xsinC2
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.1
Explore 12 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.2
Explore 8 Videos
- PROGRESSION AND SERIESBook:CENGAGEChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBook:CENGAGEChapter:PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEExercise:Question Bank
Explore 32 Videos
Similar Questions
In ABC, as semicircle is inscribed, which lies on the side ⋅ If x is the lengthof the angle bisector through angle C, then prove that the radius of the semicircle is xsin(C2).
View SolutionIn a ΔABC, a semicircle is inscribed, whose diameter lies on the side c. Then the radius of the semicircle is (Where Δ is the area of the triangle ABC)
View Solution
Knowledge Check
A semicircle is inscribed inside a rectangle in such a way, so that the diameter semicides with the length of the rectangle. If the area of the semicircle is 50π, then what is area of the rectangle?
(a)200
(b)175
(c)150
(d)125A200πB175πC150πD125πIn a triangle with sides, a,b, and c a semicircle toughing the sides AC and CB is inscribed whose diameter lies on AB. Then the radius of the semicricel is
Aa/2BΔ/sC2Δa+bD2abc(s)(a+b)cosA2cosB2cosC2Find the value of ∠A. If BD is an interior angle bisector of ∠B and DC is an exterior angle bisector of ∠C.
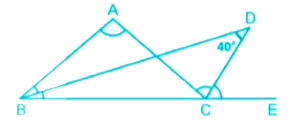 A70∘B60∘C80∘D110∘
A70∘B60∘C80∘D110∘
Let a≤b≤c be the lengths of the sides of a triangle. If a2+b2<c2, then prove that triangle is obtuse angled .
View SolutionPQ is a vertical tower having P as the foot. A,B,C are three points in the horizontal plane through P. The angles of elevation of Q from A,B,C are equal and each is equal to θ . The sides of the triangle ABC are a,b,c, and area of the triangle ABC is . Then prove that the height of the tower is (abc) tanθ4.
View SolutionIn an acute angle triange ABC, a semicircle with radius ra is constructed with its base on BC and tangent to the other two sides rbandrc are defined similarly. If r is the radius of the incircle of triangle ABC then prove that 2r=1ra+1rb+1rc
View SolutionThe sides of a triangle ABC are 6, 7, 8, the smallest angle being C then
The length of internal bisector of angle C is …
View SolutionA right angle triangle whose hypotenuse is c and its perpendicular sides are a and b. Three semicircles are drawn along the three sides of this triangle in such a way that the diameter of each semicircle is equal to the length of the respective side of the triangle. The semicircle drawn wiht the help of hypotenuse intersects the other two semicircles as shown in the concerned diagram. Find the area of the shaded region.
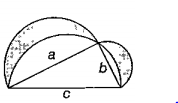
View Solution