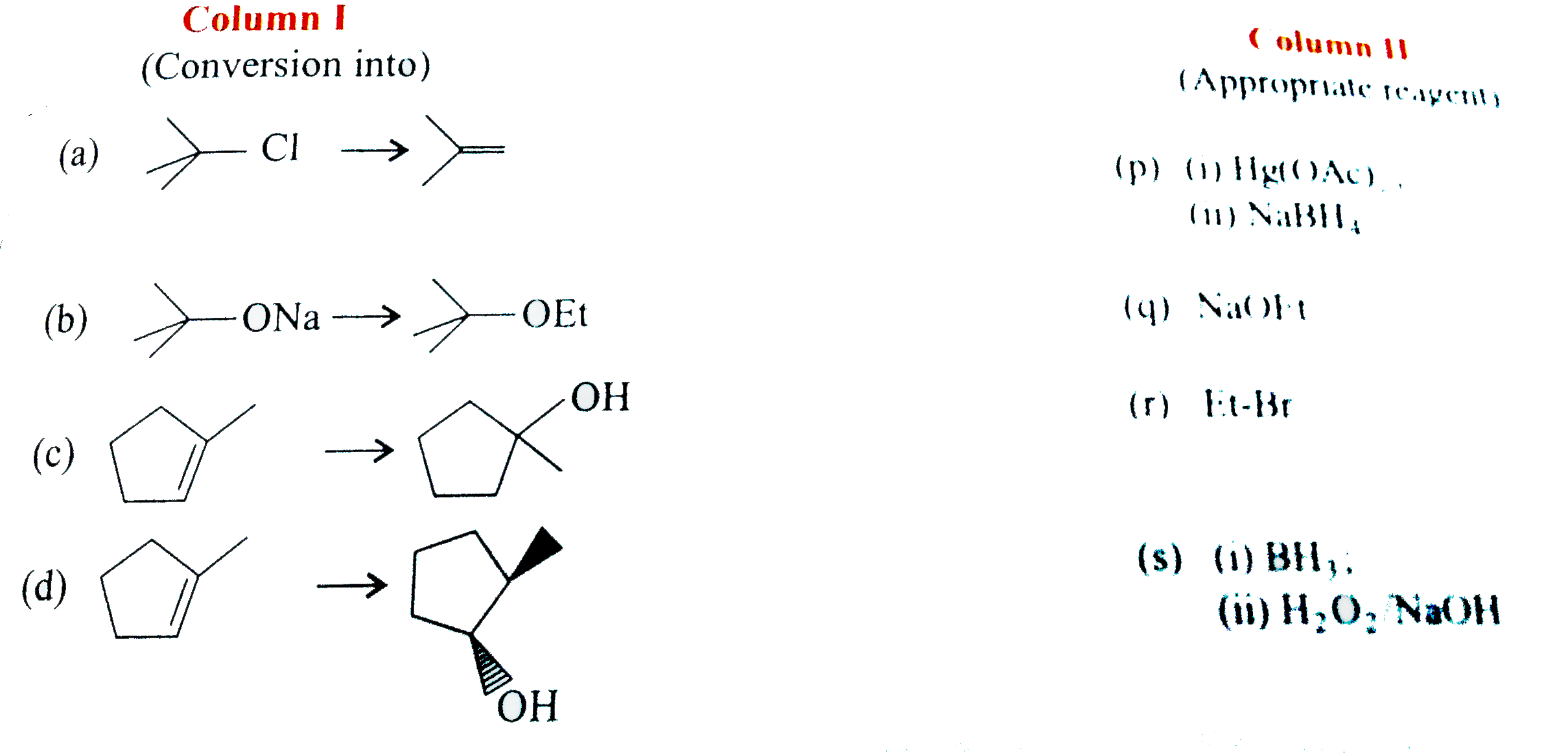
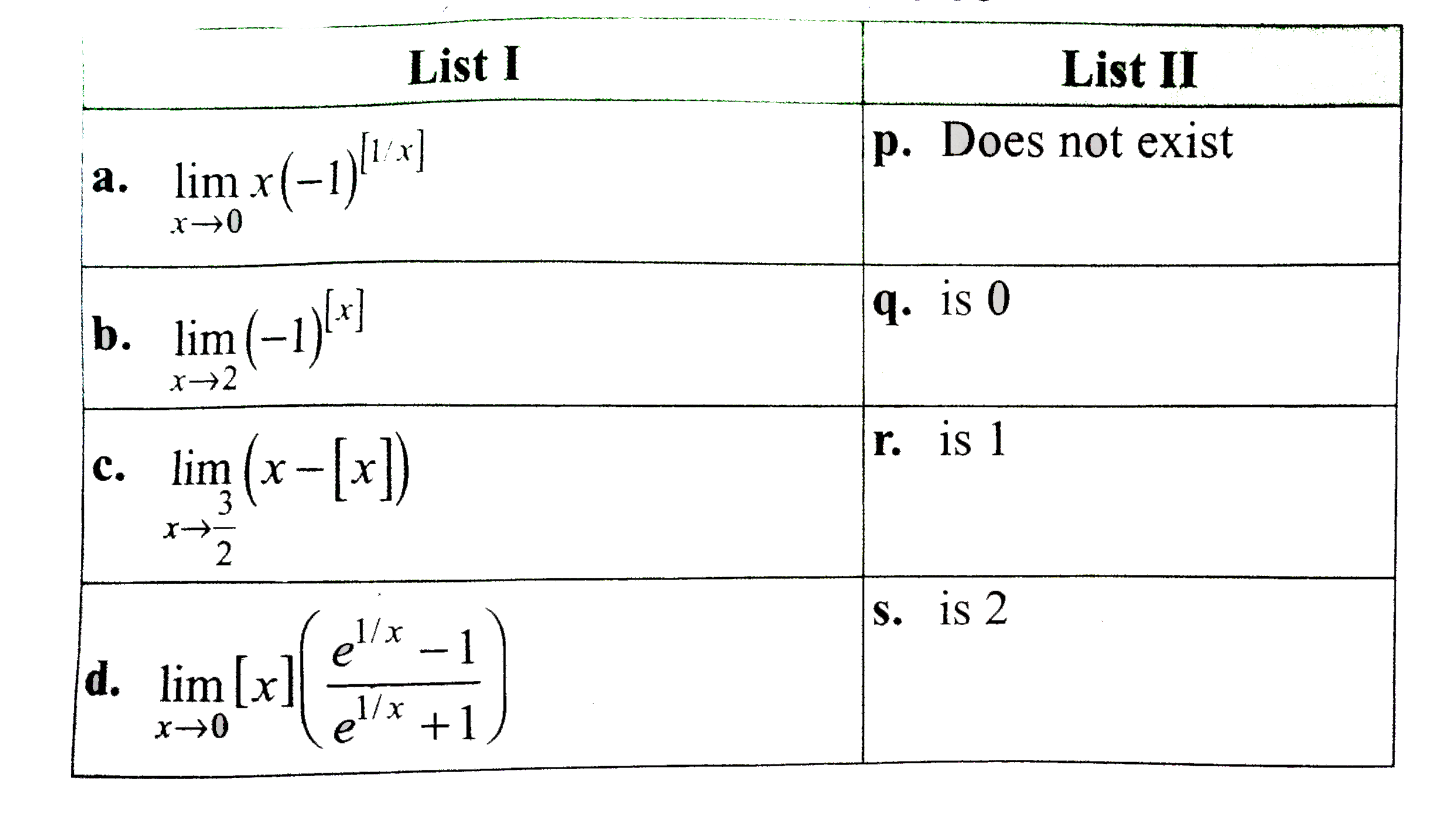
Consider
$\int \frac{x^{3} + 3 x^{2} + 2 x + 1}{\sqrt{x^{2} + x + 1}} d x$
$= (a x^{2} + b x + c) \sqrt{x^{2} + x + 1} + λ \int \frac{d x}{\sqrt{x^{2} + x + 1}}$
Now, match the following lists and then choose the correct code.
$Consider int(x^(3)+3x^(2)+2x+1)/(sqrt(x^(2)+x+1))dx =(ax^(2)+bx+c)sqrt(x^(2)+x+1)+lambda int(dx)/(sqrt(x^(2)+x+1)) Now, match the following lists and then choose the correct code. Codes: {:(,a,b,c,d),((1),q,p,s,r),((2),s,p,q,r),((3),r,q,p,s),((4),q,s,p,r):}$
Codes:
$\begin{matrix} a & b & c & d (1) & q & p & s & r (2) & s & p & q & r (3) & r & q & p & s (4) & q & s & p & r \end{matrix}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:4

$\int \frac{x^{3} + 3 x^{2} + 2 x + 1}{\sqrt{x^{2} + x + 1}} d x$
$= (a x^{2} + b x + c) \sqrt{x^{2} + x + 1} + λ \int \frac{d x}{\sqrt{x^{2} + x + 1}}$
Differentiating both side, we get
$\frac{x^{3} + 3 x^{2} + 2 x + 1}{\sqrt{x^{2} + x + 1}} = \frac{(a x^{2} + b x + c) (2 x + 1)}{2 \sqrt{x^{2} + x + 1}} + (2 a x + b) \sqrt{x^{2} + x + 1} + λ \frac{1}{\sqrt{x^{2} + x + 1}}$
$= \frac{6 a x^{3} + (5 a + 4 b) x^{2} + (4 a + 3 b + 2 c) x + (c + 2 b + 2 λ)}{2 \sqrt{x^{2} + x + 1}}$
Now, compare coefficients on both sides and solve equations.

Updated on:21/07/2023

|

Class 12 MATHS INDEFINITE INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

If $P = \int_{1}^{2} (\frac{\sqrt{x^{2} + 1} + x - 1}{\sqrt{x^{2} + 1} + x + 1}) d x$ and
$Q = \int_{1}^{2} (\frac{x}{\sqrt{x^{2} + 1 + 1}}) d x$ then $\frac{P}{Q}$ is equal
A $I n \frac{2}{5}$
B $\frac{2}{3}$
C $\frac{1}{2}$
D1
$\int \frac{1}{x + \sqrt{x^{2} - x + 1}} d x = P log (x + \sqrt{x^{2} - x + 1}) + Q log (2 x - 1 + 2 \sqrt{x^{2} - x + 1}) + R (\frac{3}{2 x - 1 + 2 \sqrt{x^{2} - x + 1}}) + c$
Then the values of P, Q, R are
A $2, \frac{3}{2}, \frac{1}{2}$
B $2, - \frac{3}{2}, \frac{1}{2}$
C $2, - \frac{3}{2}, - \frac{1}{2}$
DNone of these

CENGAGE-INDEFINITE INTEGRATION-Exercise (Matrix)

Home
Ask Doubt
Profile