Question

If $\int \frac{x^2-x+1}{{(x^2+1)}^{\frac{3}{2}}}{e}^{x}dx=e^{x}f\left(x\right)+c,then$

$f\left(x\right)$
is an even function
$f\left(x\right)$
is a bounded function
the range of $f\left(x\right)$
is $(0,1)$

$f\left(x\right)$
has two points of extrema

Options

A. `f(x)` is an even function
B. `f(x)` is a bounded function
C. the range of `f(x)` is (0, 1]
D. `f(x)` has two points of extrema

Answer

A::B::C

Explanation

`I=int (x^(2)-x+1)/((x^(2)+1)^(3//2))e^(x)dx`
`=inte^(x)[(x^(2)+1)/((x^(2)+1)^(3//2))-(x)/((x^(2)+1)^(3//2))]dx`
`=int e^(x)[(1)/(sqrt(x^(2)+1))+{(-x)/((x^(2)+1)^(3//2))}]dx`
`=e^(x)[f(x)+f'(x)]dx, " where "f(x)=(1)/(sqrt(x^(2)+1))`
`=e^(x) f(x)+c=(e^(x))/(sqrt(x^(2)+1))+c`
The graph of `f(x)` is given in the figure.

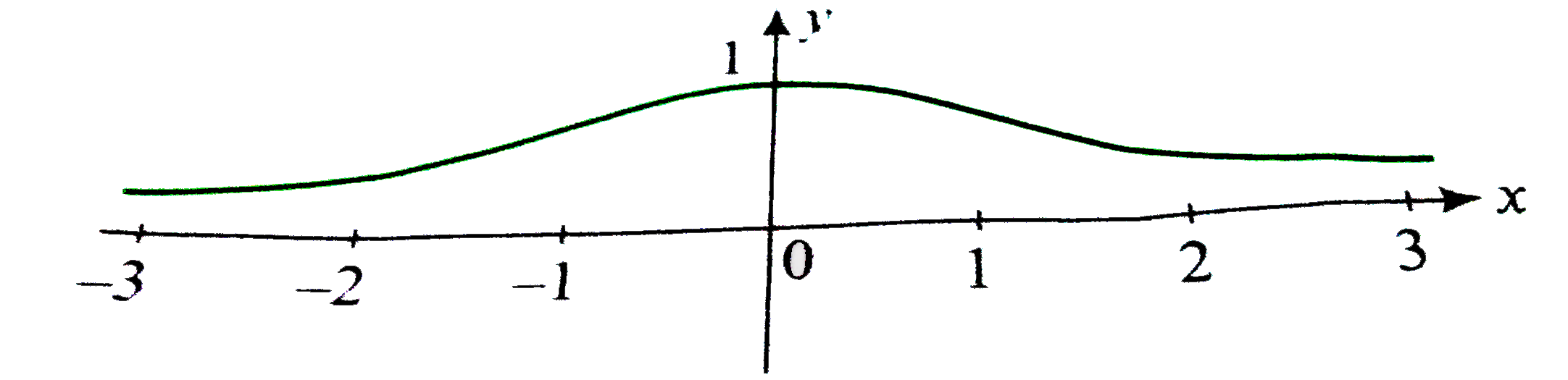
From the graph, `f(x)` is even, bounded function and has the range (0, 1].