A flexible conducting wire in the form of a circle is kept in a uniform magnetic field with its plane normal to the field. Radius of that circle changes with time as shown. Then which of the following graphs represents the variation of induction emf with time R=R0,t<t0,R=R0+t,t0<t<2t0:

A

B

C

D

Video Solution
Text Solution
The correct Answer is:C
|
Answer
Step by step video, text & image solution for A flexible conducting wire in the form of a circle is kept in a uniform magnetic field with its plane normal to the field. Radius of that circle changes with time as shown. Then which of the following graphs represents the variation of induction emf with time R = R_(0), t lt t_(0) , R = R_(0) + t, t_(0) lt t lt 2t_(0): by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
- BOOK - NARAYNACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION & REASON6videos
ELECTROMAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-324videos
ELECTROMAGNETIC INDUCTION
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - LEVEL-II(H.W)14videos
ELECTRO MAGNETIC WAVES
- BOOK - NARAYNACHAPTER - ELECTROMAGNETIC WAVES EXERCISE - EXERCISE -415videos
ELECTROMAGNETIC WAVES
Knowledge Check
- Question 1 - Select One or More
Which of the following graphs represents zero order if
A→P
At t=0⇒[A]0
At t=t⇒[A]tA B
B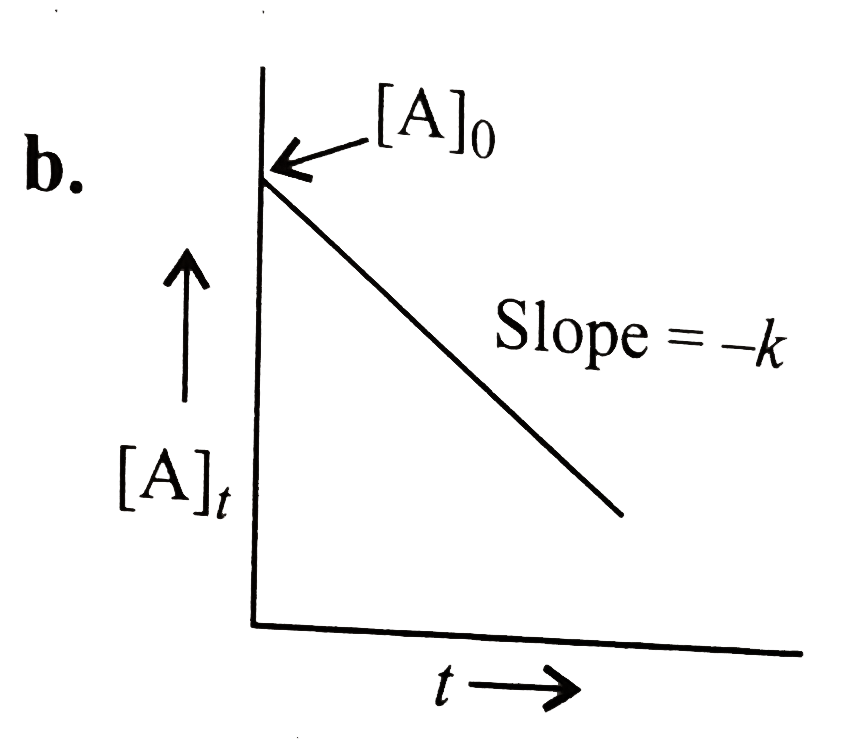 C
C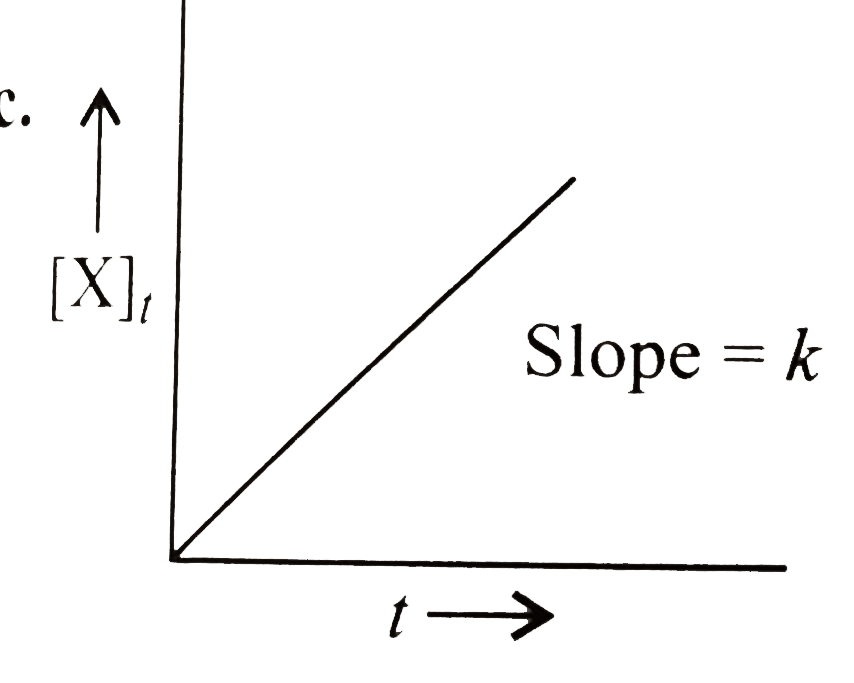 D
D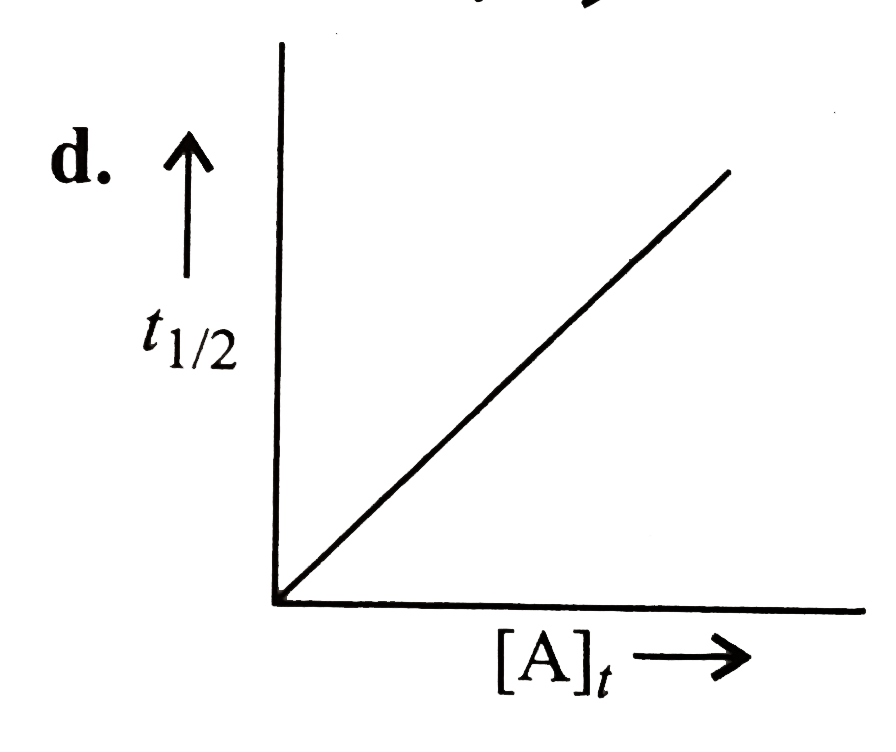
- Question 1 - Select One
A conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
 A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero
A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero - Question 1 - Select One
a conducting loop of radius R is precent in a uniform magnetic-field B perpendicular the plane of the ring. If radius R varies as a function of time 't', as R0+t. The e.m.f induced in the loop is
 A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero
A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero - Question 1 - Select One
A circular wire loop of radius r lies in a uniform magnetic field B, with its plane perpendicular to magnetic field. If the loop is deformed to a square shape in the same plane in time t, the emf induced in the loop is
AπBr2t(1−π2)BπBr2t(1−π3)CπBr2t(1−π4)DπBr2t(1−π5) - Question 1 - Select One
A conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of ring. If radius R varies as a function of time t as R=R0+t2. The emf induced in the loop is
 A2πBt(R0+t2) ClockwiseB2πBt(R0+t2) AnticlockwiseC4πBt(R0+t2) AnticlockwiseD4πBt(R0+t2) Clockwise
A2πBt(R0+t2) ClockwiseB2πBt(R0+t2) AnticlockwiseC4πBt(R0+t2) AnticlockwiseD4πBt(R0+t2) Clockwise - Question 1 - Select One
Radius of a circular ring is changing with time and the coil is placed in uniform magnetic field perpendicular to its plane. The variation of 'r' with time 't' is shown in Fig. Then induced emf e with time t will be best represented by
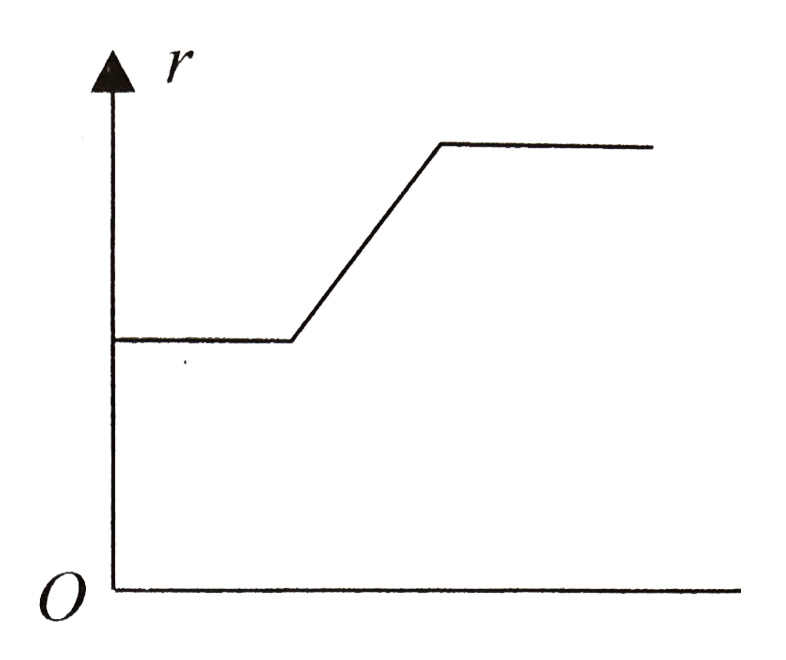 A
A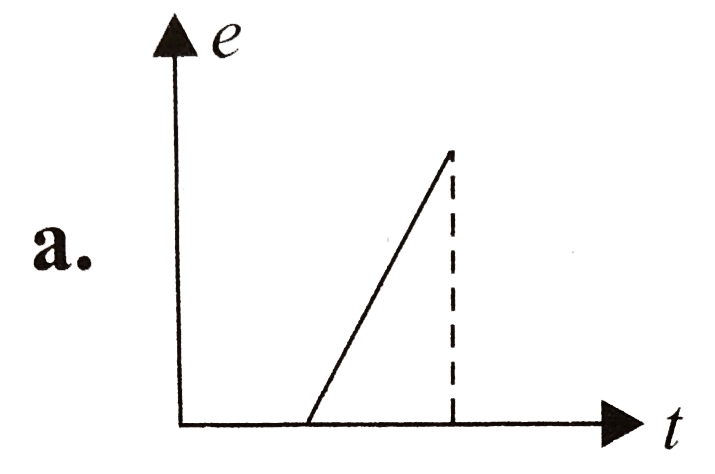 B
B C
C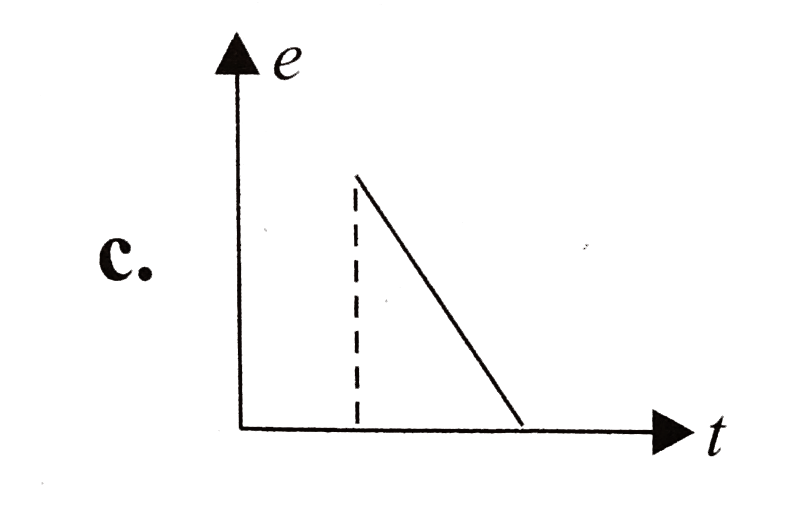 D
D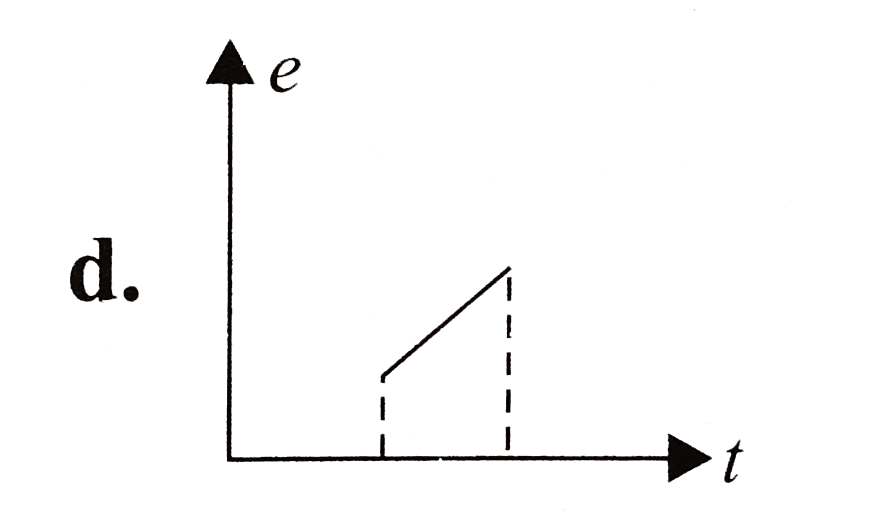
- Question 1 - Select One
A square loop of side 22cm is changed to a circle in time 0.4sec with its plane normal to a magnetic field 0.2T. The emf induced is
A+6.6mvB−6.6mvC+13.2mvD−13.2mv - Question 1 - Select One
A square loop of side 44 cm is changed to a circle in time 0.5 sec with its plane normal to a magnetic field 0.6 T. The emf induced is
A0.5 VB0.4 VC0.2 VD0.6 V - Question 1 - Select One
A flexible wire bent in the form of a circle is placed in a uniform magnetic field perpendicular to the plane of the coil. The radius of the coil changing as shown in figure. The graph of induced emf in the coil is represented by
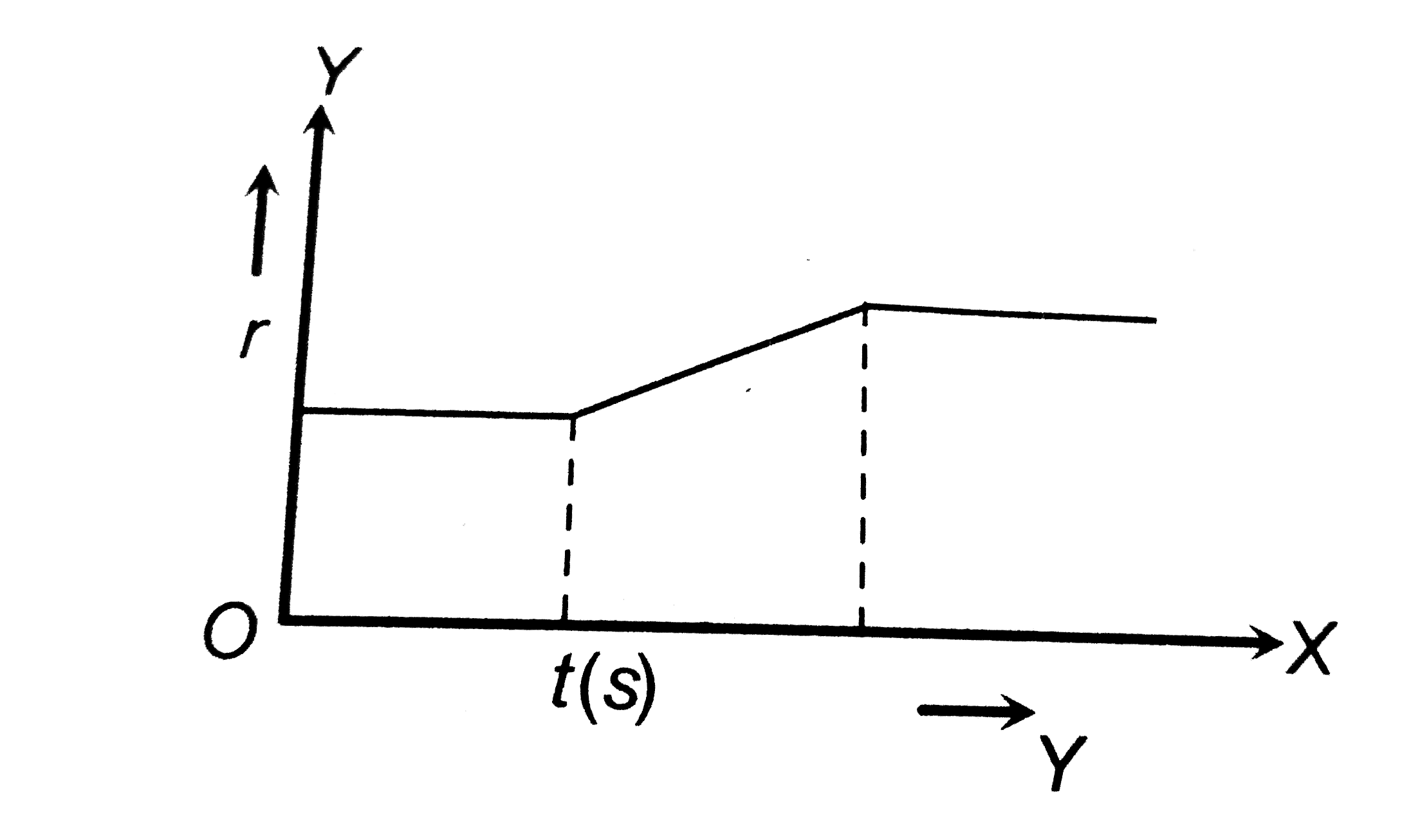 A
A B
B C
C D
D


