In a circular motion of a particle the tangential acceleration of the particle is given by at=2tm/s2. The radius of the circle described is 4m. The particle is initially at rest. Time after which total acceleration of the particle makes 45∘ with radial acceleration is :
1s
2s
3s
12s
The correct Answer is:B
Step by step video & text solution for In a circular motion of a particle the tangential acceleration of the particle is given by a_(t) = 2t m//s^(2). The radius of the circle described is 4m. The particle is initially at rest. Time after which total acceleration of the particle makes 45^(@) with radial acceleration is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
In a circular motion of a particle , the tangential acceleration of the particle is given by at=9ms−2 . The radius of the circle is 4m . The particle was initially at rest. Time after which total acceleration of the particle makes an angle of 45∘ with the radial acceleration is
View SolutionIn a circular motion of a particle , the tangential acceleration of the particle is given by at=9ms−2 . The radius of the circle is 4m . The particle was initially at rest. Time after which total acceleration of the particle makes an angle of 45∘ with the radial acceleration is
View Solution
Knowledge Check
The tangenital acceleration of a particle in a circular motion of radius 2 m is at=αtm/s2 (where α is a constant) initially the particle as rest. Total acceleration of the particle makes 45∘ with the radial acceleration after 2 sec The value of constant α is :
A12m/s3B1m/s3C2m/s3DData are insufficientStarting from rest, acceleration of a particle is a=2t(t−1). The velocity of the particle at t=5s is
AAt t=2s, the position of the particle is at x=9mBParticle acceleration at t=2s is 1m/s2CParticle acceleration is 1/2m/s2 through out the motionDParticle will never go in negative direction from it's starting positionThe displacement 'x' of a particle moving along a straight line at time t is given by x=a0+a1t+a2t2. The acceleration of the particle is :-
Aa8Ba1Ca3D2a2
Tangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30∘ with radial acceleration is
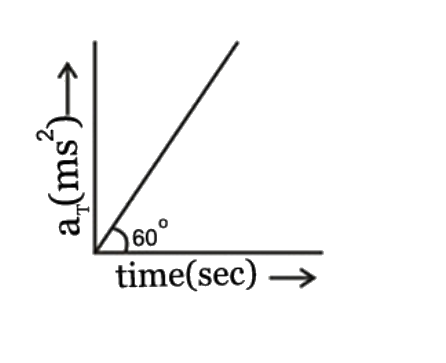
View SolutionA particle is moving on a circular path of radius 1m. It starts from rest,its tangential acceleration is √3t .The time after which the acceleration of the particle makes an angle of 30∘ with centripetal acceleration is (n)23s .Find the value of n.
View SolutionThe tangential and radial acceleration of a particle are a(t) and a(r) respectively. The motion of a particle is circular if
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View SolutionThe distance in seconds, described by a particle in t seconds is given by s=aet+bet. The acceleration of the particle at time t is
View Solution
