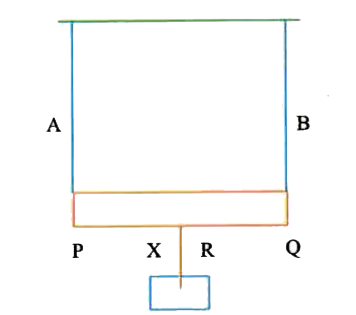
A rod PQ of length 'L' is hung from two identical wires A and B. A block of mass 'm' is hung at point R of the rod as shown in figure. The value of 'x' so that the fundamental mode in wire A is in resonance with first overtone of B is
4L5
L4
L5
2L3
The correct Answer is:C
fA=2fB,12l√TAμ=22l√TBμ⇒TA=4TB
→τ=→r×→f= constant, TATB=4=l−xx
Topper's Solved these Questions
Similar Questions
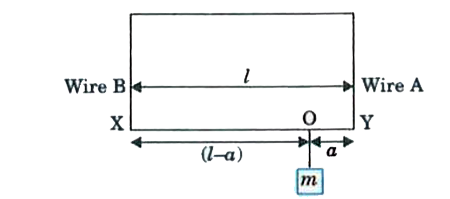
From two identical wires, a rod XY of length l is hung. A wooden block of mass m is hung at point O of the rod at a distance a from wire A. Find the value of a in the case when a tuning fork excites the fundamental note in wire A and third harmonic in wire B.
View SolutionTwo identical rods each of mass m and length are connected as shown. Locate c.m.
View Solution
Knowledge Check
A massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
_E01_188_Q01.png) Al5Bl4C4l5D3l4
Al5Bl4C4l5D3l4A light rod of length L is suspended from a support horizonatlly by means of two vertical wires A and B of equal lengths as show in the figure . Cross-section area of A is half that of B and Young's modulus of A is double than that of B. A weight W is hung on the rod as shown. The value of x, so that the stress In A is same as that in B,is
 AL3BL2C2L3D3L4
AL3BL2C2L3D3L4A massless rod BD is suspended by two identical massless strings AB and CD of equal lengths. A block of mass m is suspended at point P such that BP is equal to x, If the fundamental frequency of the left wire is twice the fundamental frequency of right wire, then the value of x is :-
_E01_188_Q01.png) Al2Bl3Cl4Dl5
Al2Bl3Cl4Dl5
A uniform rod of length l and mass m is hung from, strings of equal length from a ceiling as shown in figure. Determine the tensions in the strings?

View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
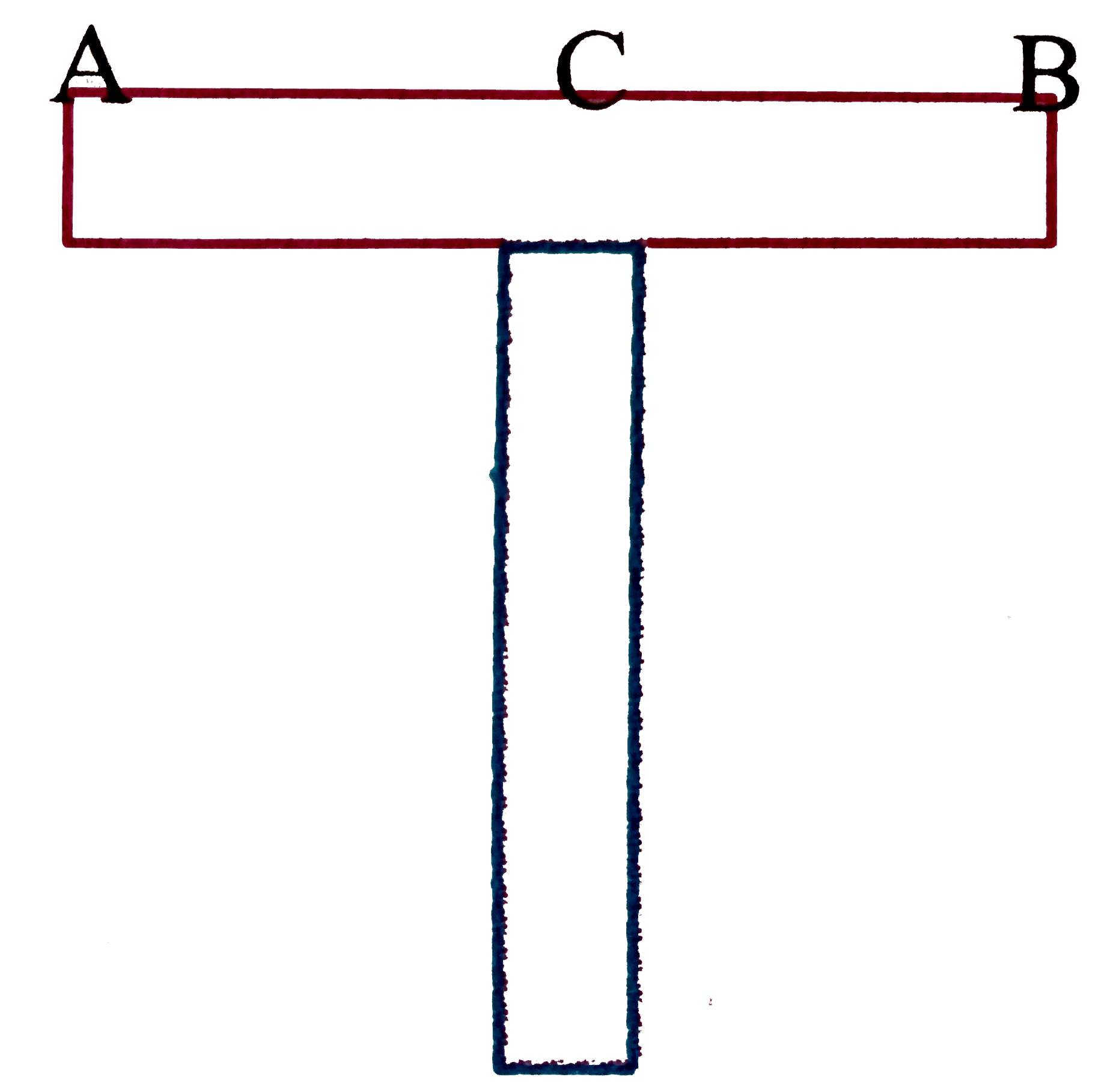
View SolutionTwo identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
View SolutionA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is

View SolutionA uniform horizontal rod of length l falls vertically from height h on two identical blocks placed symmertrically below the rod as shown in figure the coefficients of restitution are e1 and e2 the maximum height through which the centre of mass of the rod will rise after after bouncing off the blocks is

View Solution
