If a vibrating tuning fork of frequency 255Hz is approaching with a velocity 4m/s perpendicular to a wall. The number of beats produced per sec is (speed of sound in air =340m/s)
3
4
5
6
The correct Answer is:D
To solve the problem, we need to find the number of beats produced per second when a tuning fork of frequency 255 Hz is approaching a wall at a velocity of 4 m/s. The speed of sound in air is given as 340 m/s.
1. Identify the Given Values:
- Frequency of the tuning fork (ν) = 255 Hz
- Velocity of the tuning fork (vs) = 4 m/s (approaching the wall)
- Speed of sound in air (v) = 340 m/s
2. Determine the Apparent Frequency (ν'):
When the source of sound (tuning fork) is moving towards a stationary observer (the wall), the apparent frequency can be calculated using the formula:
ν′=ν(vv−vs)
Here, since the tuning fork is approaching the wall, we subtract the source velocity from the speed of sound.
3. Substituting the Values:
ν′=255(340340−4)
Simplifying the denominator:
340−4=336
Thus, we have:
ν′=255(340336)
4. Calculating the Apparent Frequency:
ν′=255×1.00714≈258 Hz
(Using a calculator, 340336≈1.00714)
5. Calculate the Number of Beats:
The number of beats produced per second is the difference between the apparent frequency and the original frequency:
Number of beats=ν′−ν=258 Hz−255 Hz=3 Hz
Final Answer:
The number of beats produced per second is 3 Hz.
---
- Frequency of the tuning fork (ν) = 255 Hz
- Velocity of the tuning fork (vs) = 4 m/s (approaching the wall)
- Speed of sound in air (v) = 340 m/s
When the source of sound (tuning fork) is moving towards a stationary observer (the wall), the apparent frequency can be calculated using the formula:
ν′=ν(vv−vs)
Here, since the tuning fork is approaching the wall, we subtract the source velocity from the speed of sound.
ν′=255(340340−4)
Simplifying the denominator:
340−4=336
Thus, we have:
ν′=255(340336)
ν′=255×1.00714≈258 Hz
(Using a calculator, 340336≈1.00714)
The number of beats produced per second is the difference between the apparent frequency and the original frequency:
Number of beats=ν′−ν=258 Hz−255 Hz=3 Hz
The number of beats produced per second is 3 Hz.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-II (C.W)15videos
WAVES
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-II (H.W)17videos
WAVES
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-I (C.W)104videos
WAVES
- BOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-II (H.W)14videos
VECTORS
- BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV43videos
WORK , ENERGY & POWER
Similar Questions
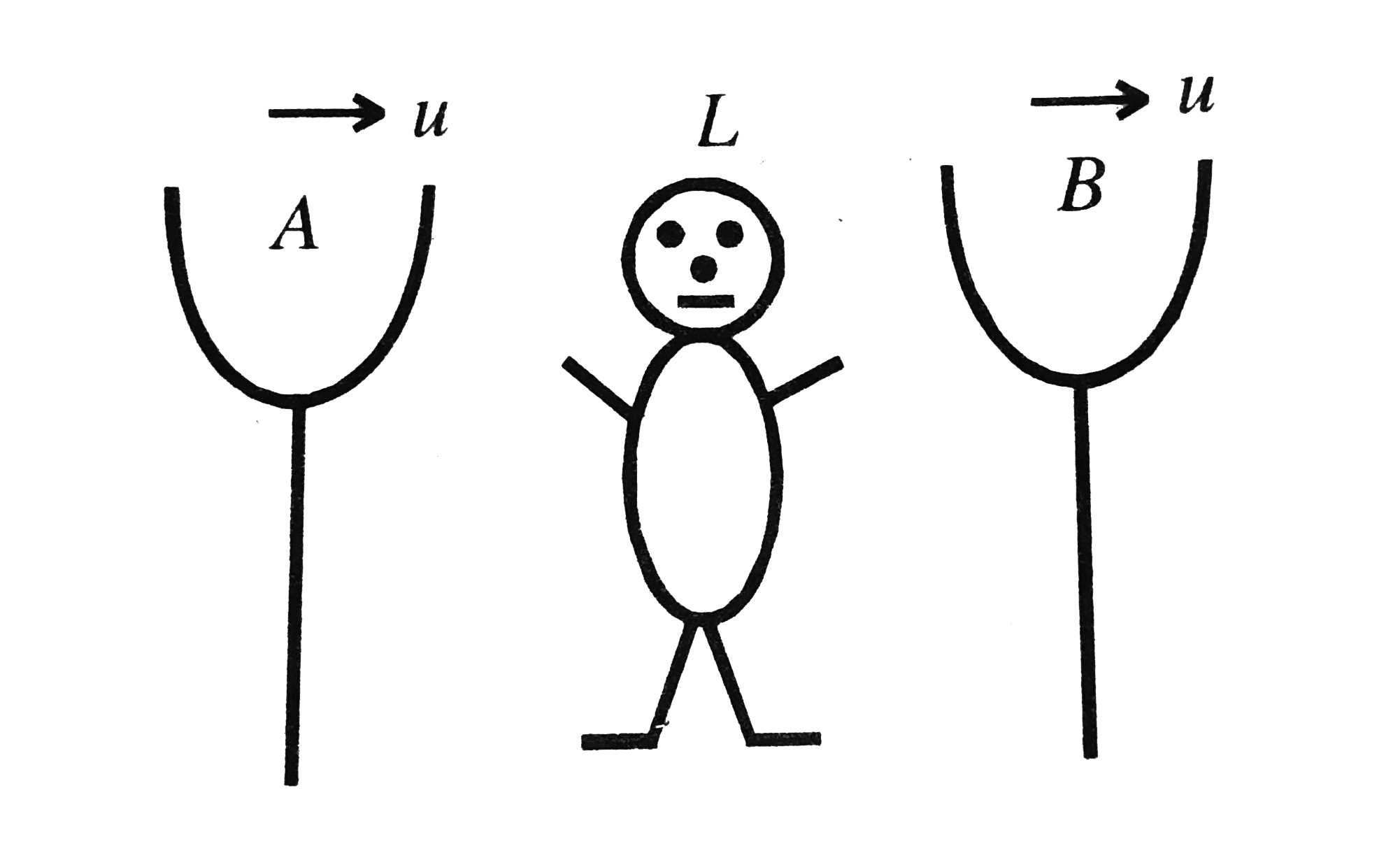Two tuning forks A and B are vibrating at the same frequency 256 Hz. A listener is standing midway between the forks. If both tuning forks move to the right with a velocity of 5ms, find the number of beats heard per second by the listerner (speed of sound in air is 330ms).View SolutionThe velocity of sound in air, in water and in a given solid is, 330ms−1,1350ms−1 and 1500ms−1, respectively. If a vibrating tuning fork of frequency 150 Hz is placed in each of these media, then find the distance covered by the sound in air, water and solid, respectively, at the end of 50 vibrations.
View Solution
Knowledge Check
- Question 1 - Select One
A man is running with a fork of frequency 340 Hz towards a huge wall with a velocity 2m/s, then the number of beats heard per second is (Velocity of sound in air is 342 m/s)
A2B6C4D8 - Question 2 - Select One
A man holding a tuning fork of frequency 90 hertz runs straight towards a stationary wall with velocity of 3.7 m/sec. The number of beats per second heard by him is (Speed of sound in air =340m/s.)
A10B20CzeroD2 - Question 3 - Select One
A vibrating string of certain length l under a tension T resonates with a maode corresponding to the first overtone (third harmonic) of an air column of length 75cm inside a tube closed at one end. The string also gereates 4 beats per second when excited along with a tuning fork of frequency n. now when the tension of the string is slightly increased the number of beats reduces 2 per second. assuming the velocity of sound in air ti be 340m/s, the frequency n of the tuning fork in Hz is
A(a) 344B(b) 336C( c ) 117.3D( d ) 109.3
If a tuning fork of frequency 512Hz is sounded with a vibrating string of frequency 505.5Hz the beats produced per sec will be
View Solution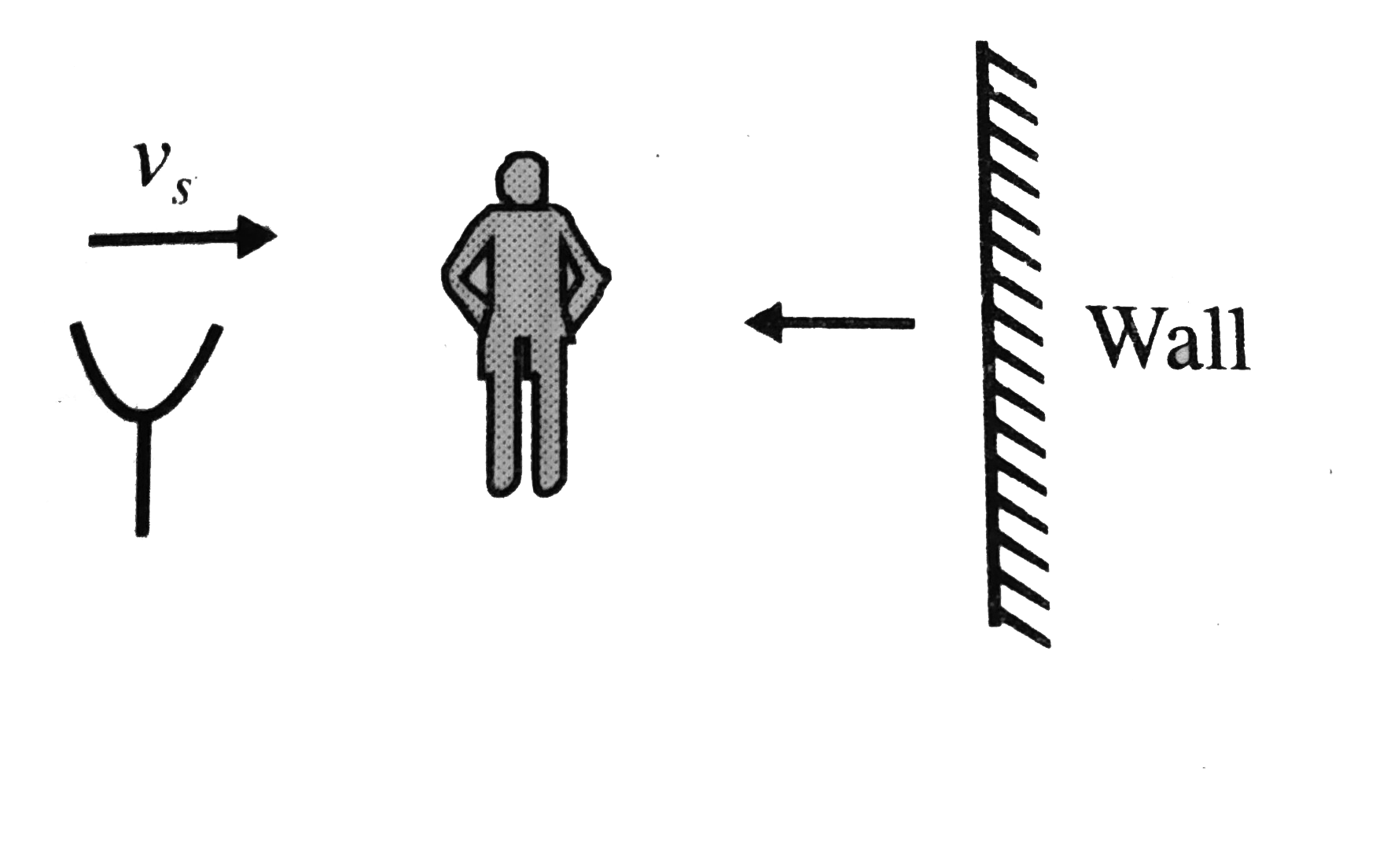
A tuning fork of frequency 380 Hz is moving towards a wall with a velocity of 4ms Then the number of beats heard by a stationary listener between direct and reflected sound will be (velocity of sound in air is 340ms)View SolutionA cylindrical pipe of length 29.5cm closed at one end is found to be in resonance when a tuning fork of frequency 864Hz is sounded near the open end. Then the mode of vibration of the air in the pipe is (Velocity of sound in air is 340m/s.)
View SolutionA car blowing a horn of frequency 350 Hz is moving normally towards a wall a speed of 5 m/s The beat frequency heard by a person standing between the car and wall is (speed of sound in air =350 m/s )
View Solution
As shown if Fig. a vibrating tuning fork of frequency 512 Hz is moving towards the wall with a speed 2ms. Take speed of sound as v=340ms and answer the following questions.
Q. Suppose that a listener is located at rest between the tuning fork and the wall. Number of beats heard by the listener per second will beView Solution