Two different sound sources and have frequencies in the ratio . Source is approaching towards observer and receding from same observer. Speeds of both and are V each and speed of sound air is . If no beats are heard by the observer then the value of V is
The correct Answer is:C
To solve the problem, we need to use the concept of the Doppler effect, which describes how the frequency of a wave changes for an observer moving relative to the source of the wave.
1. Identify the Frequencies:
Let the frequency of source S1 be f and the frequency of source S2 be 2f (since the ratio is 1:2).
2. Doppler Effect for Source S1 (approaching the observer):
The apparent frequency f′ heard by the observer when source S1 is approaching is given by:
f′=fvsvs−v
where vs is the speed of sound in air (330 m/s) and v is the speed of source S1.
3. Doppler Effect for Source S2 (receding from the observer):
The apparent frequency f′′ heard by the observer when source S2 is receding is given by:
f′′=2fvsvs+v
4. Condition for No Beats:
Since no beats are heard, the two frequencies must be equal:
f′=f′′
Substituting the expressions for f′ and f′′:
fvsvs−v=2fvsvs+v
5. Cancel f:
Since f is common on both sides and is not zero, we can cancel it:
vsvs−v=2vsvs+v
6. Cross Multiply:
Cross multiplying gives:
vs(vs+v)=2vs(vs−v)
7. Expand and Simplify:
Expanding both sides:
v2s+vsv=2v2s−2v
Rearranging terms:
vsv+2v=2v2s−v2s
vsv+2v=v2s
8. Solve for v:
Rearranging gives:
vsv=v2s−2v
vsv+2v=v2s
v(vs+2)=v2s
v=v2svs+2
9. Substituting vs=330m/s:
v=3302330+2=108900332≈327.11m/s
10. Final Calculation:
Since we need v to be a fraction of vs:
v=3303=110m/s
Conclusion:
The speed V of both sources S1 and S2 is 110m/s.
Let the frequency of source S1 be f and the frequency of source S2 be 2f (since the ratio is 1:2).
The apparent frequency f′ heard by the observer when source S1 is approaching is given by:
f′=fvsvs−v
where vs is the speed of sound in air (330 m/s) and v is the speed of source S1.
The apparent frequency f′′ heard by the observer when source S2 is receding is given by:
f′′=2fvsvs+v
Since no beats are heard, the two frequencies must be equal:
f′=f′′
Substituting the expressions for f′ and f′′:
fvsvs−v=2fvsvs+v
Since f is common on both sides and is not zero, we can cancel it:
vsvs−v=2vsvs+v
Cross multiplying gives:
vs(vs+v)=2vs(vs−v)
Expanding both sides:
v2s+vsv=2v2s−2v
Rearranging terms:
vsv+2v=2v2s−v2s
vsv+2v=v2s
Rearranging gives:
vsv=v2s−2v
vsv+2v=v2s
v(vs+2)=v2s
v=v2svs+2
v=3302330+2=108900332≈327.11m/s
Since we need v to be a fraction of vs:
v=3303=110m/s
The speed V of both sources S1 and S2 is 110m/s.
Topper's Solved these Questions
- WAVESBook:NARAYNAChapter:WAVESExercise:Exercise-I (H.W)
Explore 101 Videos
- WAVESBook:NARAYNAChapter:WAVESExercise:Exercise-II (C.W)
Explore 15 Videos
- WAVESBook:NARAYNAChapter:WAVESExercise:C.U.Q
Explore 68 Videos
- VECTORSBook:NARAYNAChapter:VECTORSExercise:LEVEL-II (H.W)
Explore 14 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE IV
Explore 43 Videos
Similar Questions
A source of sound of frequency n is moving towards a stationary observer with a speed S. If the speed of sound in air is V and the frequency heard by the observer is n1 ,the value of n1/n is
View Solution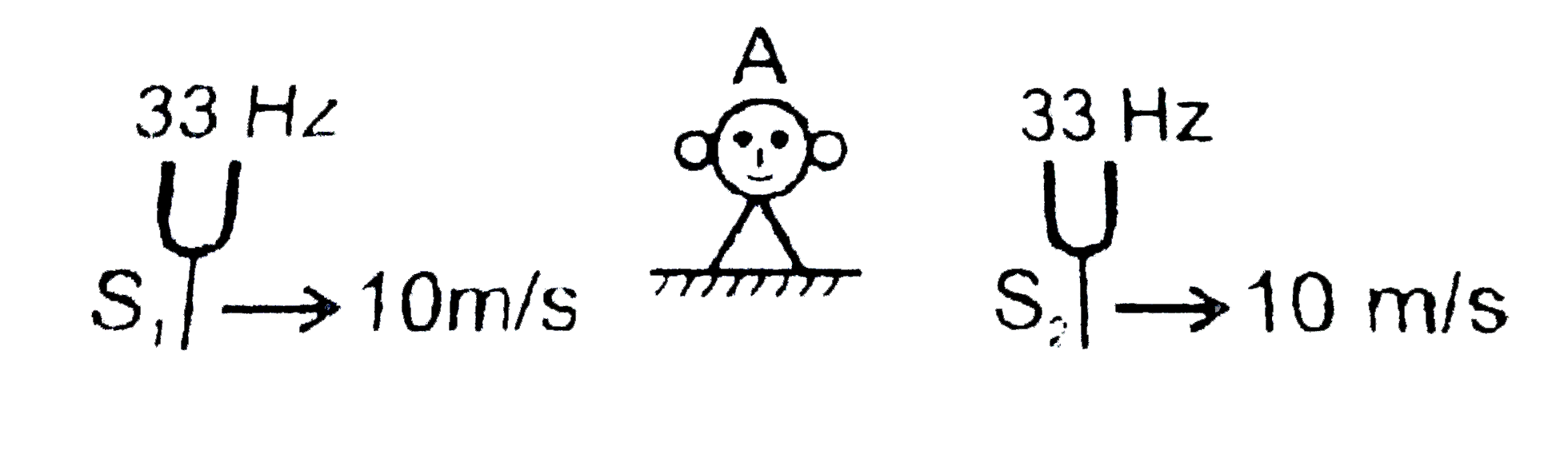
Observer A is at rest. Source S1 is moving towards observer A and source S2 is moving away from observer A. velocity of sound is 330msec. β= beat frequency heard per second by A. Approximate value of β is:
View Solution
Knowledge Check
Consider the vehicle emitting sound wave of frequency 700 Hz moving towards an observer at a speed 22ms−1 . Assuming the observer to be at rest, and speed of sound to be 330ms−1 , the frequency of sound as measured by the observer is
A25254HzB19603HzC22403HzD750HzA whistle emitting a sound of frequency 450 Hz approaches a stationary observer at a speed of 33 m/s. Velocity of sound is 330 m/s. The frequency heard by the observer, in Hz, is :
A409B429C517D500A source is moving towards an observer with a speed of 20 m / s and having frequency of 240 Hz . The observer is now moving towards the source with a speed of 20 m / s . Apparent frequency heard by observer, if velocity of sound is 340 m / s , is
A240 HzB270 HsC280 HzD360 Hz
A source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionA source of sound of frequency 500 Hz is moving towards a stationary observer with velocity 30m/s. The speed of sound is 330m/s. The frequency heard by the observer will be :
View SolutionA source of sound of frequency 500 Hz is moving towards a stationary observer with velocity 30m/s. The speed of sound is 330m/s. The frequency heard by the observer will be :
View SolutionThe sources S1 is at rest. The observer and the source S2 are moving towards S1 as shown in figure. The roof beats observed by the observer if both sources have frequency 120 Hz and speed of sound 330m/s in is
_PHY_E01_016_Q01.png)
View SolutionThe ratio of the apparent frequencies of a car when approaching and receding a stationary observer is 11:9 What is the speed of the car, if the velocity of sound in air is 330 m/s?
View Solution