Two soap bubble of radii R1 and R2 are kept in vacuum at constant temperature, the ratio of masses of air inside them, is
From, PV=mMRT i.e., m∝PV
P1=P0+4TR1=0+4TR1,P2=P0+4TR2=0+4TR2
m1m2=P1V1P2V2=(4TR1)43πR31(4TR2)43πR32∴m1m2=R21R32
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:EVALUATE YOURSELF - 1
Explore 2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:EVALUATE YOURSELF - 2
Explore 2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Level 2 (H.W)
Explore 39 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBook:NARAYNAChapter:MATHEMATICAL REVIEW & PHYSICAL WORLDExercise:C.U.Q
Explore 13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
Two soap bubble of radii R1 and R2 are in atmosphere of pressure P0 at constant temperature. Ratio of masses of air inside them is
View SolutionTwo small metallic balls of radii R1&R2 are kept in vacuum at a large distance compared to the radii. Find the ratio between the charges on the two balls at which electrostatic energy of the system is minimum. What is the potential difference between the two balls ? total charge of balls is constant.
View Solution
Knowledge Check
Two soap bubbles of radii R1andR2 kept in atmosphere are combined isothermally to form a big bubble of radius R. The expression for surface tension will be
AP0(R3+R31+R32)4(R2+R21+R22)BP0(R31+R32−R3)4(R2−R21−R22)CP0(R31+R32−R3)D4P0(R31+R32−R3)Two spheres of radii R1 and R2 are made of the same material and are at the same temperature. The ratio of their thermal capacities is:
AR41/R42BR31/R32CR21/R22DR1/R2Two metal spheres of radii R1 and R2 are charged to the same potential. The ratio of charges on the spheres is
A√R1:√R2BR1:R2CR21:R22DR31:R32
Two soap bubbles of radii r1andr2 are attached as shown. Find the radius of curvature of the common film ACB.
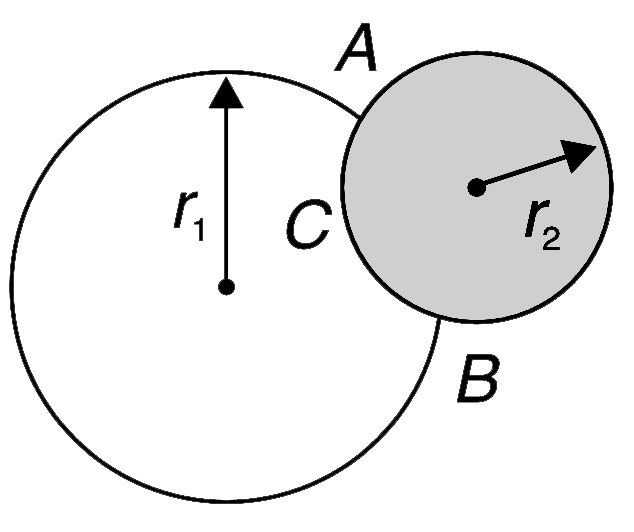
View SolutionUnder isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
View SolutionTwo soap bubbles of radius r1 and r2 combine. Find radius of curvature of the common surface separating them.

View SolutionThe radii of two soap bubbles are R1 and R2 respectively. The ratio of masses of air in them will be
View SolutionTwo soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
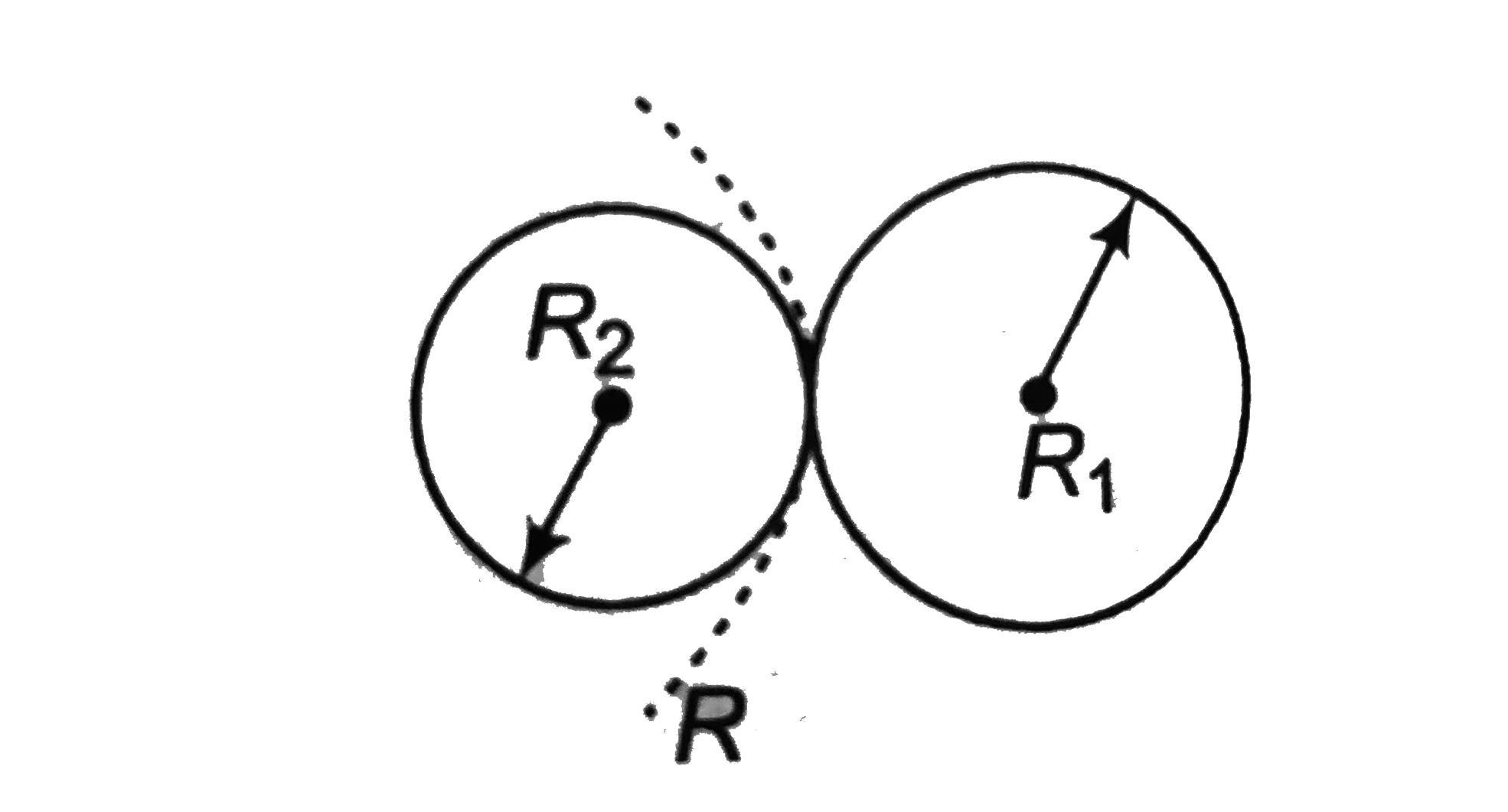 .
.
View Solution

