Two bodies of masses 2kg and 4 kg are moving with velocities 20 m/s and 10m/s towards each other due to mutual gravitational attraction . What is the velocity of their centre of mass ?
5.3ms−1
6.4ms−1
Zero
8.1ms−1
The correct Answer is:C
To find the velocity of the center of mass of the two bodies, we can use the formula for the velocity of the center of mass (V_cm) for a system of particles:
Vcm=m1v1+m2v2m1+m2
Where:
- m1 and m2 are the masses of the two bodies,
- v1 and v2 are the velocities of the two bodies.
1. Identify the masses and velocities:
- Mass of body 1, m1=2kg
- Velocity of body 1, v1=20m/s (towards the right)
- Mass of body 2, m2=4kg
- Velocity of body 2, v2=−10m/s (towards the left, hence negative)
2. Substitute the values into the formula:
Vcm=(2kg×20m/s)+(4kg×−10m/s)2kg+4kg
3. Calculate the numerator:
Vcm=(40kg m/s)+(−40kg m/s)6kg
=0kg m/s6kg=0m/s
4. Conclusion:
The velocity of the center of mass of the system is 0m/s.
- m1 and m2 are the masses of the two bodies,
- v1 and v2 are the velocities of the two bodies.
- Mass of body 1, m1=2kg
- Velocity of body 1, v1=20m/s (towards the right)
- Mass of body 2, m2=4kg
- Velocity of body 2, v2=−10m/s (towards the left, hence negative)
Vcm=(2kg×20m/s)+(4kg×−10m/s)2kg+4kg
Vcm=(40kg m/s)+(−40kg m/s)6kg
=0kg m/s6kg=0m/s
The velocity of the center of mass of the system is 0m/s.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EVALUATE YOURSELF - 3
Explore 4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EVALUATE YOURSELF - 5
Explore 6 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EVALUATE YOURSELF - 4
Explore 11 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (H.W.)
Explore 19 Videos
Similar Questions
2 bodies of different masses of 2 kg and 4 kg are moving with velocities 20m/s and 10 m//s towards each other due to mutual gravitational attraction. What is the velocity of their centre of mass?
View SolutionTwo bodies of masses 2 kg and 4 kg are moving with velocities 2 m/s and 10 m/s respectively along same direction. Then the velocity of their centre of mass will be
View Solution
Knowledge Check
Two bodies of masses 2 kg and 4 kg are moving with velocities 2 m s−1 and 10 m s−1 towards each other due to mutual gravitational attraction. What is the velocity of their centre of mass?
A5.3ms−1B6.4ms−1CzeroD8.1ms−1Two bodies of different masses 2kg and 4kg are moving with velocities 2m/s and 10m/s towards each other due to mutual gravitational attraction. Then the velocity of the centre of mass is
A5ms−1B6ms−1C8ms−1Dzero2 bodies of different masses of 2 kg and 4 kg are moving with velocities 20m/s and 10 m//s towards each other due to mutual gravitational attraction. What is the velocity of their centre of mass?
A5ms−1B6ms−1C8ms−1DZero
Two particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionA body of mass 8 kg is moving with a velocity of 4 m/s, find its momentum.
View SolutionTwo bodies of masses 1kgand2kg are moving in two perpendicular direction with velocities 1m/sand2m/s as shown in figure. The velocity of the centre of mass (in magnitide) of the system will be :
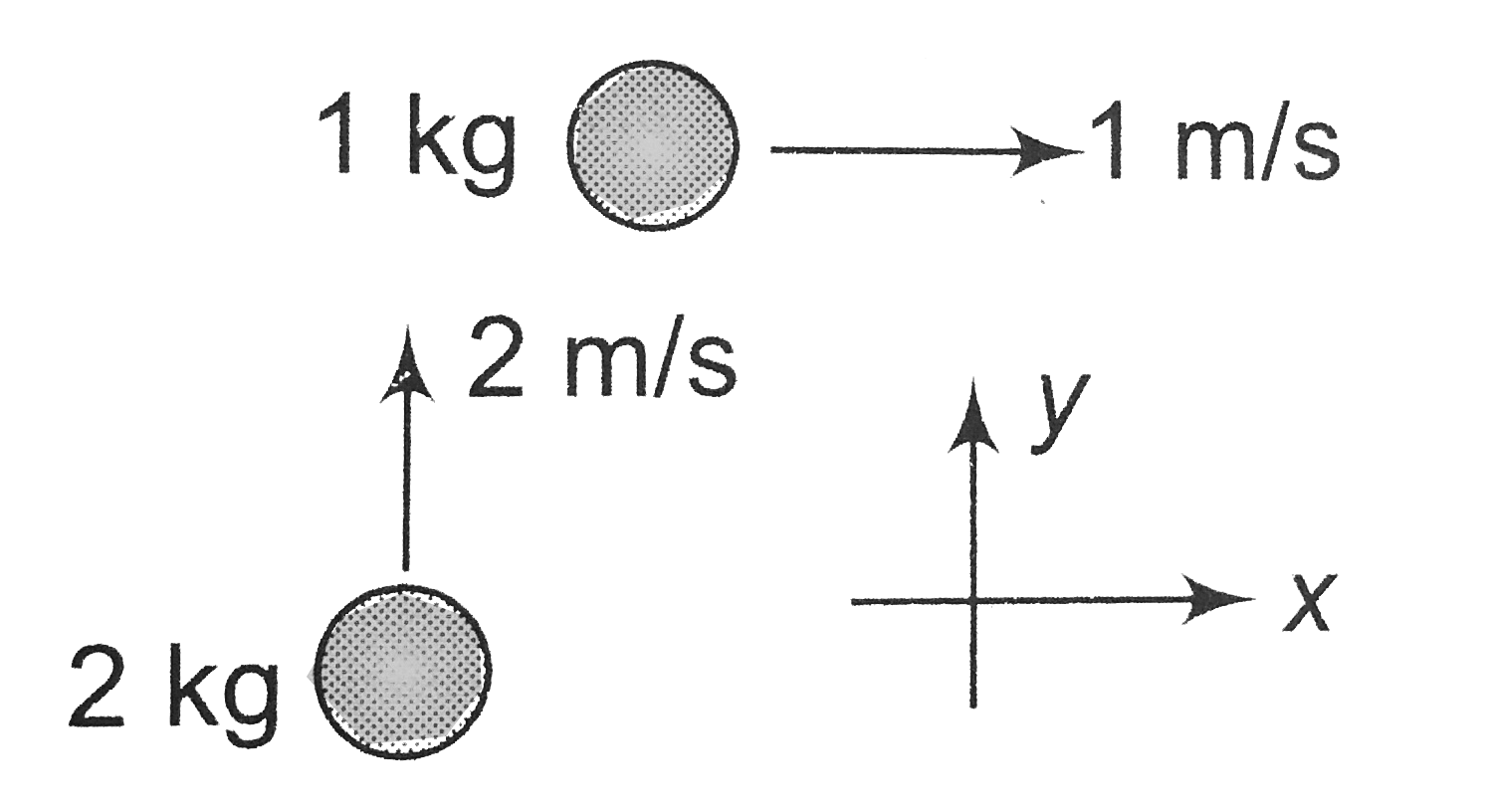
View SolutionTwo objectes of mass m and 4m are at rest at and infinite seperation. They move towards each other under mutual gravitational attraction. If G is the universal gravitational constant. Then at seperation r
View Solution

