A body is undergoing circular motion. Some vector expression that describe the motion are given below
(a)
(b)
(c )
Of the above statements following are/is correct
a, b and c
a and b
b and c
c and a
The correct Answer is:B
To solve the problem, we need to analyze the given vector expressions related to circular motion and determine which of them are correct. Let's break down the statements one by one.
Step 1: Analyze Statement (a)
The first statement is:
→V=→ω×→R
Where:
- →V is the linear velocity vector.
- →ω is the angular velocity vector.
- →R is the radial vector (position vector from the center of the circular path to the particle).
In circular motion, the linear velocity →V of a particle is indeed given by the cross product of the angular velocity →ω and the radial vector →R. This statement is correct.
Step 2: Analyze Statement (b)
The second statement is:
→aT=→α×→R
Where:
- →aT is the tangential acceleration vector.
- →α is the angular acceleration vector.
Tangential acceleration is related to the change in angular velocity over time. The correct expression for tangential acceleration is given by:
→aT=α⋅→R
This means that the tangential acceleration is directly proportional to the angular acceleration and not through a cross product. Therefore, this statement is incorrect.
Step 3: Analyze Statement (c)
The third statement is:
→aC=→α×→R
Where:
- →aC is the centripetal acceleration vector.
Centripetal acceleration is directed towards the center of the circular path and is given by:
→aC=V2R (or equivalently, ω2RR=ω2R)
It is not expressed as a cross product with angular acceleration. Therefore, this statement is also incorrect.
Conclusion
From the analysis:
- Statement (a) is correct.
- Statement (b) is incorrect.
- Statement (c) is incorrect.
Thus, the correct statements are:
- Only statement (a) is correct.
Final Answer
The correct answer is: Only statement (a) is correct.
The first statement is:
→V=→ω×→R
Where:
- →V is the linear velocity vector.
- →ω is the angular velocity vector.
- →R is the radial vector (position vector from the center of the circular path to the particle).
The second statement is:
→aT=→α×→R
Where:
- →aT is the tangential acceleration vector.
- →α is the angular acceleration vector.
→aT=α⋅→R
This means that the tangential acceleration is directly proportional to the angular acceleration and not through a cross product. Therefore, this statement is incorrect.
The third statement is:
→aC=→α×→R
Where:
- →aC is the centripetal acceleration vector.
→aC=V2R (or equivalently, ω2RR=ω2R)
It is not expressed as a cross product with angular acceleration. Therefore, this statement is also incorrect.
From the analysis:
- Statement (a) is correct.
- Statement (b) is incorrect.
- Statement (c) is incorrect.
- Only statement (a) is correct.
The correct answer is: Only statement (a) is correct.
Topper's Solved these Questions
- LAW OF MOTIONBook:NARAYNAChapter:LAW OF MOTIONExercise:C.U.Q
Explore 73 Videos
- LAW OF MOTIONBook:NARAYNAChapter:LAW OF MOTIONExercise:EXERCISE - I (C.W)(NEWTON.S LAWS OF MOTION)
Explore 8 Videos
- LAW OF MOTIONBook:NARAYNAChapter:LAW OF MOTIONExercise:EVALUATE YOURSELF - 4
Explore 9 Videos
- KINETIC THEORY OF GASESBook:NARAYNAChapter:KINETIC THEORY OF GASESExercise:LEVEL-III(C.W)
Explore 52 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBook:NARAYNAChapter:MATHEMATICAL REVIEW & PHYSICAL WORLDExercise:C.U.Q
Explore 13 Videos
Similar Questions
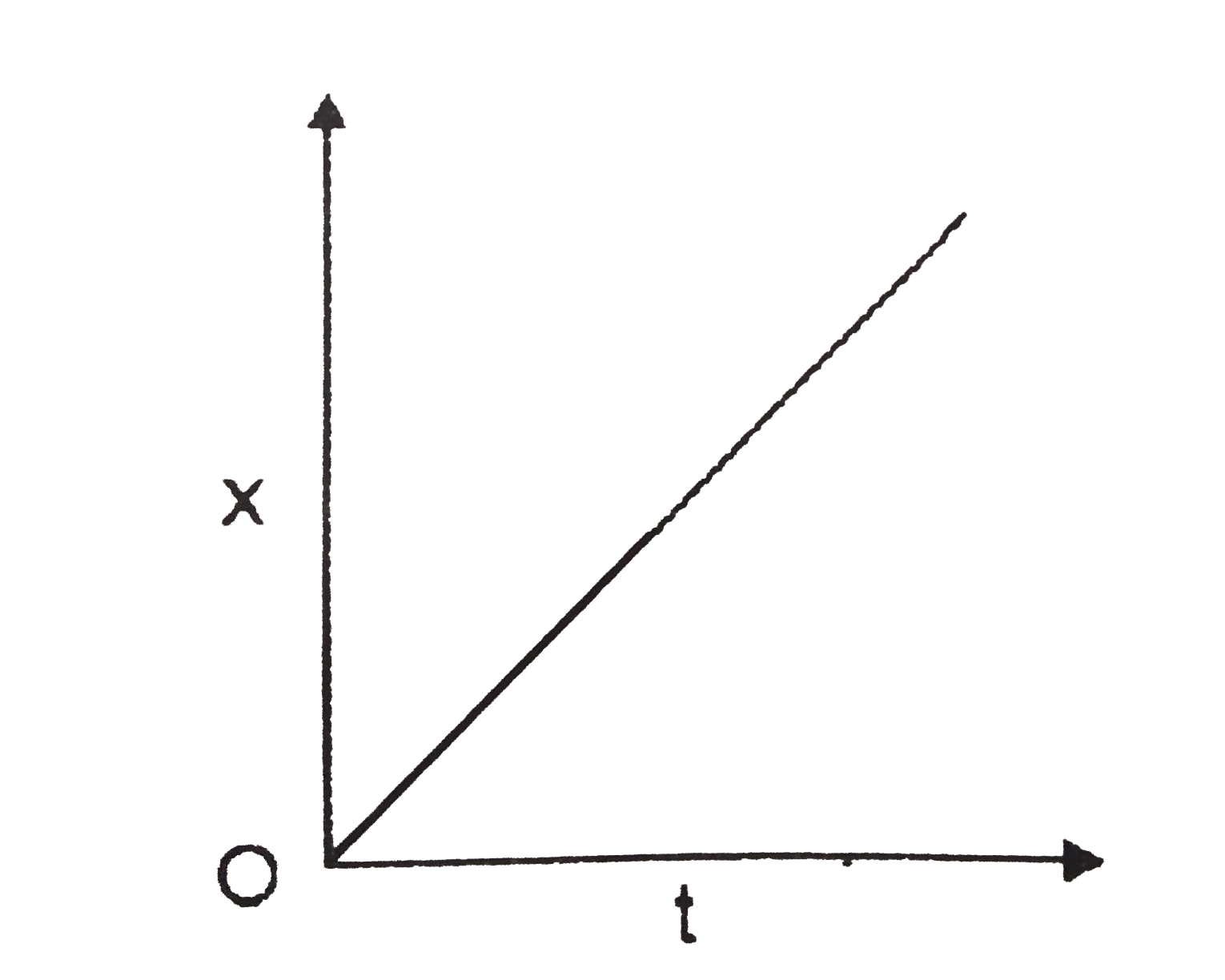
The motion of a particle is given by a straight line in the graph given above drawn with displacement (x) and time (t). Which one among the following statements is correct ?
View SolutionLet →a=3ˆi+ˆj+2ˆkand→b=ˆi−2ˆj−4ˆk be the positon vectors of the points A and B respectively. If →r is the position vector of any point P(x,y,z) on the plane passing through the point A and perpendiculr to the line AB, then consider the following statements: The locus of →r=xˆi+yˆj+zˆk is given by 1. (→r.→a).(→b−→a)=0 2. (→r−→a).(→a−→b)=0 3. 2x+3y+6z−21=0 Which of the statements given above are correct? (A) 1,2,and 3 (B) 1 and 2 (C) 1 and 3 (D) 2 and 3
View Solution
Knowledge Check
A particle is undergoing a non - uniform circular motion about the point O (origin).
Read the following statements carrefully (here the symbols have their usual meanings)
a) −→aTand→v are always in the same line
b) −→aT,→vand−→aC are always in the same line
c) →αand→ω are always in the same line
d) →p,→vand→aT are always in the same line
e) →Land→ω are always in the same line
f) The net liner acceleration and angular acceleration are always perpendicular to each other
g) →r (radius vector) −→aC are along the same line Out of the above statements, the following are correctAa, c, d, e and gBa, c, d, e, f and gCd, e, f and gDe, f and gFor a body, angular velocity →ω=ˆi−2ˆj+3ˆk and radius vector →r=ˆi+ˆj+ˆk, then its velocity (→v=→ω×→r) is :
A−5ˆi+2ˆj+3ˆkB−5ˆi+2ˆj−3ˆkC−5ˆi−2ˆj+3ˆkD−5ˆi−2ˆj−3ˆkLet →a,→b,→c be three non-coplanar vectors and →p,→q,→r be the vectors defined by the relations.
→p=→b×→c[→a→b→c],→q=→c×→a[→a→b→c],→r=→c×→a[→a→b→c]
Then the value of the expression
(→a+→b).→p+(→b+→c).→q+(→c+→a).→r is equal toA0B1C2D3
In U.C.M. (Uniform Circular Motion), prove the relation →υ=→ω×→r, where symbols have their usual meanings.
View SolutionIn U.C.M. (Uniform Circular Motion), prove the relation →υ=→ω×→r, where symbols have their usual meanings.
View SolutionFind the value of ∣∣→V∣∣ if the linear velocity of a rotating body is given by →v=→ω×→r, where →ω is the angular velocity and →r is the radius vector. The angular velocity of a body is
→ω=ˆi−2ˆj and the radius vector
→r=2ˆj−3ˆk.
View SolutionLet the vectors −−→PQ,−−→QR,−−→RS,−→ST,−−→TU and −−→UP represent the sides of a regular hexagon.
Statement I:−−→PQ×(−−→RS+−→ST)≠→0
Statement II: −−→PQ×−−→RS=→0 and −−→PQ×−−→RS=→0 and −−→PQ×−→ST≠→0
For the following question, choose the correct answer from the codes (A), (B) , (C) and (D) defined as follows:
View SolutionLet →r,→a,→b and →c be four non zero vectors such that →r.→a=0,∣∣→r×→b∣∣=|→r|∣∣→b∣∣ and |→r×→c|=|→r||→c| . Then [abc] is equal to
View Solution

