एक अर्द्धवृत्तीय चाप, जिसकी त्रिज्या a है, को आवेशित किया गया। रेखीय आवेश घनत्व λ है, तो चाप के केन्द्र पर वैद्युत क्षेत्र की तीव्रता का मान होगा
λ2πε0a
λ2πε0a2
λ4π2ε0a
λ22πε0a
The correct Answer is:A
बिन्दु A व B पर dl लम्बाई का सममित अवयव लेते हैं तथा PO के लम्बवत् अवयव एक-दूसरे को निरस्त कर देते हैं।
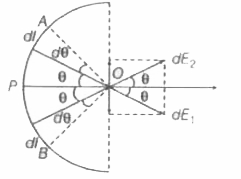
dl अवयव के कारण विद्युत क्षेत्र,
dE=14πε0dqa2cosθ
=14πε0λdla2cosθ
=14πε0λ(adθ)a2cosθ [∵dl=adθ]
O पर कुल विद्युत क्षेत्र,
E=∫π/2−π/2dE=2∫π/2014πε0λacosθdθa2
=214πε0lamda(sinθ)π/20
=2.14πε0.λa.1=λ2πε0a
Topper's Solved these Questions
Similar Questions
चित्र में दो धनात्मक आवेश q2 व q3, Y-अक्ष के अनुदिश स्थापित है , x-अक्ष के अनुदिश स्थापित q1 आवेश पर धनात्मक X-दिशा में एक परिणामी बल लगाते है यदि धनात्मक आवेश Q को (x,0) पर जोड़ा जाता है, तो q1 पर बल
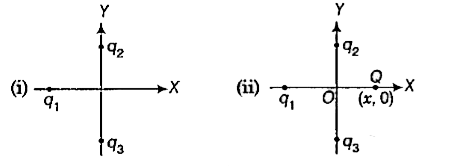
View Solutionतीन तरंगें A,B और C जिनकी आवृत्ति 1600 Hz, 5 MHz और 60 MHz हैं, एक स्थान से दूसरे स्थान पर भेजी जाती हैं, निम्नलिखित में से कौन-सी अति उपयुक्त संचार की विधि है?
View Solutionआवेशित वलय के कारण विद्युत क्षेत्र की तीव्रता
View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionयदि बिंदु (3,4) समीकरण 3y=ax+6 के आलेख पर स्थित है , तो a का मान होगा :
View SolutionIf the value of gravitational acceleration on the earth plane 10 मीटर/ Second ^ 2 है तो इसका मान प्रथ्वी के केन्द्र पर क्या होगा ( यदि प्रथ्वी को R त्रिज्या एंव एकसमान घनत्व का गोला मान लिया जाये)
View Solutionधारावाहिक चाप के कारण चुंबकीय क्षेत्र|वृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionकूलॉम नियम के महतवपूर्ण तथ्य|कूलॉम के नियम की सीमा|वैद्युत क्षेत्र|वैद्युत क्षेत्र की तीरवता|परीक्षण आवेश|वैद्युत क्षेत्र की तीरवता|बिंदु आवेश के कारण वैद्युत क्षेत्र की तीरवता|OMR|Summary
View Solutionविभिन्न आवेश वितरण के कारण विद्युत क्षेत्र तीव्रता - आवेश का वितरण|बिंदु आवेश|रेखिया आवेश|वलय के केन्द्रो अवाम अक्ष पर|विद्युत् क्षेत्र में आवेशित कण|OMR
View Solutionवैधुत क्षेत्र क्या होता है#!#एक बिंदु आवेश के लिए वैधुत क्षेत्र का सूत्र व प्रशन
View Solutionआवेश का वितरण कितने प्रकार का होता है #!#रेखीये आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता
View Solutionरेखीये आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता पर आधारित प्रश्न
View Solutionप्रश्न |विद्युत क्षेत्र |बिन्दु आवेश के कारण विद्युत क्षेत्र की तीव्रता |विद्युत क्षेत्र की तीव्रता की गुण |प्रश्न |एक समरूप आवेशित वलय के कारण विद्युत क्षेत्र |OMR|Summary
View Solution

