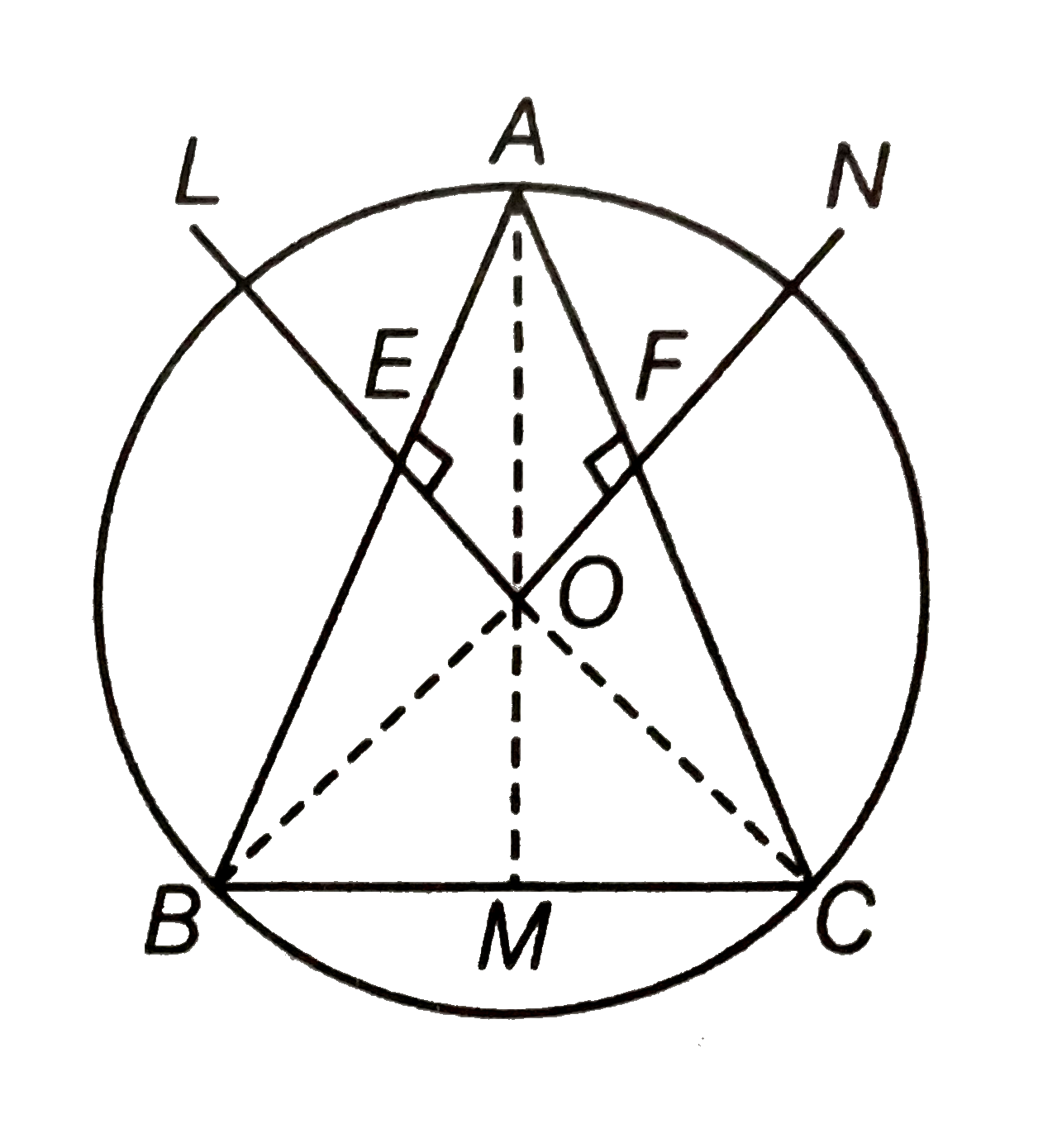
From a point O inside a triangle ABC, perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB, respectively. Prove that the perpendiculars from A, B and C to the sides EF, FD and DE are concurrent

Video Solution

Text Solution

Verified by Experts

Let the position vectors of points A,B,C,D,E and F be $\to a, \to b, \to c, \to d, \to e and \to f$ w.r.t O. Let perpendiculars from A to EF and from B to DF meet each other at H. let position vectors of H be $\to r$ . We join CH. In order to prove the statement given in the question. it is sufficient it is sufficient to prove that CH is prependicular to DE.
Now $a s O D ⊥ B C \Rightarrow \to d . (\to b - \to c) = 0$
$\Rightarrow \to d . \to b = \to d . \to c$
$a s O E ⊥ A C \Rightarrow \to e . (\to c - \to a) = 0 \Rightarrow \to e . \to c = \to e . \to a$
as $O F ⊥ A B \Rightarrow \to f . (\to a - \to b) = 0 \Rightarrow \to f . \to a = \to f . \to b$
Also $A H ⊥ E F \Rightarrow (\to r . \to a) . (\to e - \to f) = 0$
$\Rightarrow \to r . \to e - \to r . \to f - \to a . \to e + \to a . \to f = 0$
$and B H ⊥ F D \Rightarrow (\to r - \to b) . (\to f - \to d) = 0$
$\Rightarrow \to r . \to f - \to r . \to d - \to b . \to f + \to b . \to d = 0$
Adding (iv) and (v) , we get
$\to r . \to e - \to a . \to e + \to a . \to f - \to r . \to d - \to b . \to f + \to b . \to d = 0$
$or \to r . (\to e . \to d) - \to e . \to c + \to d . \to c = 0$ [ using (i), (ii) and (iii))]
$or (\to r - \to c) . (\to e - \to d) = 0$
$\Rightarrow - - \to C H . - - \to E D = 0 \Rightarrow C H ⊥ E D$

Updated on:21/07/2023

From a point O in the interior of a DeltaABC perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
A $A F^{2} + B D^{2} + C E^{2} = A E^{2} + C D^{2} + B F^{2}$
B $A B^{2} + B C^{2} = A C^{2}$
C $A F^{2} + B D^{2} + C E^{2} = O A^{2} + O B^{2} + O C^{2}$
D $A F^{2} + B D^{2} + C E^{2} = O D^{2} + O E^{2} + O F^{2}$
From a point O in the interior of a $Δ A B C$ perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
A $A F^{2} + B D^{2} + C E^{2} = A E^{2} + C D^{2} + B F^{2}$
B $A B^{2} + B C^{2} = A C^{2}$
C $A F^{2} + B D^{2} + C E^{2} = O A^{2} + O B^{2} + O C^{2}$
D $A F^{2} + B D^{2} + C E^{2} = O D^{2} + O E^{2} + O F^{2}$
In a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector $\to A D$ is equal to
A $\to B E + \to C F$
B $\to B E - \to C F$
C $\to C F - \to B E$
D $- \to B E - \to C F$