The filament of a light bulb has surface has area 64mm2. The filament can considered as a black body at temperature 2500 K emitting radiation like a point source when viewed form far. At night the light bulb is observed from a distance of 100 m. Assume the pupil of the eyes of the observer to be circular with radius 3 mm. Then (Take Stefan-Boltzman constant =5.67×10−8 Wm−2K−4, Wien's displacement constant =2.90×10−3 m-k, Planck's constant =6.63×10−8Wm−2K−4, Wien's displacement constant =2.90×10−3m-K, Planck's constant =6.63×10⋅−34) js, speed of light in vacumm =3.00×108ms−1)
power radiated by the filament is in the range 642 W to 645 W
radiated power entering into one of range 642 W to 3.25×10−8W
the wavelength corresponding to maximum intensity is 1160 nm
taking the average wavelength of emitted radiation to be 1740 nm, the number of photons entering per second into one eye of the observer is in the range 2.75×1011 to 2.85×1011
The correct Answer is:B, C, D
To solve the problem step by step, we will follow the outlined procedure:
Step 1: Convert the Surface Area to SI Units
The surface area of the filament is given as 64mm2. We need to convert this to square meters.
A=64mm2=64×10−6m2
Step 2: Calculate the Power Radiated by the Filament
Using the Stefan-Boltzmann law, the power radiated by a black body is given by:
P=εAσT4
For a black body, the emissivity ε=1. Thus, we have:
P=AσT4
Substituting the values:
- A=64×10−6m2
- σ=5.67×10−8W/m2K4
- T=2500K
Calculating T4:
T4=(2500)4=3.90625×1013K4
Now substituting into the power formula:
P=(64×10−6)×(5.67×10−8)×(3.90625×1013)
Calculating P:
P≈141.75W
Step 3: Calculate the Intensity of the Light at a Distance
The intensity I at a distance d from a point source is given by:
I=P4πd2
Given d=100m:
I=141.754π(100)2
Calculating I:
I≈141.7512566.37≈0.01129W/m2
Step 4: Calculate the Power Entering the Observer's Eye
The area of the observer's pupil is given by:
Apupil=πr2
Where r=3mm=3×10−3m:
Apupil=π(3×10−3)2≈2.827×10−5m2
The power P′ entering the observer's eye is given by:
P′=I⋅Apupil
Substituting the values:
P′=0.01129×2.827×10−5≈3.18×10−7W
Step 5: Convert Power to a Suitable Format
To express this in a more standard form:
P′≈3.18×10−8W
Step 6: Calculate the Number of Photons Entering the Eye
Using the average wavelength λ=1740nm=1740×10−9m:
The energy of a single photon is given by:
E=hcλ
Where h=6.63×10−34Js and c=3×108m/s.
Calculating E:
E=(6.63×10−34)(3×108)1740×10−9≈1.14×10−19J
Now, the number of photons n entering the eye per second is given by:
n=P′E
Substituting the values:
n=3.18×10−81.14×10−19≈2.79×1011
Final Answers
1. The power entering the observer's eye is approximately 3.18×10−8W.
2. The number of photons entering the observer's eye per second is approximately 2.79×1011.
The surface area of the filament is given as 64mm2. We need to convert this to square meters.
Using the Stefan-Boltzmann law, the power radiated by a black body is given by:
- σ=5.67×10−8W/m2K4
- T=2500K
The intensity I at a distance d from a point source is given by:
The area of the observer's pupil is given by:
To express this in a more standard form:
Using the average wavelength λ=1740nm=1740×10−9m:
1. The power entering the observer's eye is approximately 3.18×10−8W.
2. The number of photons entering the observer's eye per second is approximately 2.79×1011.
Topper's Solved these Questions
- JEE ADVANCED 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-3
6 Videos
- JEE ADVANCED 2020BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2020EXERCISE - SECTION-3
6 Videos
- JEE ADVANCEDBOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCEDEXERCISE - PHYSICS SECTION - IV Matrix Match Type
2 Videos
- JEE ADVANCED 2021BOOK - JEE ADVANCED PREVIOUS YEARCHAPTER - JEE ADVANCED 2021EXERCISE - QUESTION
38 Videos
Similar Questions
Put a unifrom meter scale horizontally on your extended index fingers with the left one at 0.0 cm and the right one at 90.00 cm when you attempt to move both the fingers slowly towards the center , initially only the left finger slips with respect to to the scale and the right finger does not . after some distance, the left finger stops and the right one starts slipping . Then the right finger stops at a distance XR from the center (50.00 cm ) of the scale and the left one starts slopping again . This happens because to the difference in the fiictional forces on the two fingers . it the coefficients of static and dynamic between the fingers and the scale are 0.4 and 0.32 respectively , the value of XR (in cm is ...........
View SolutionPut a unifrom meter scale horizontally on your extended index fingers with the left one at 0.0 cm and the right one at 90.00 cm when you attempt to move both the fingers slowly towards the center , initially only the left finger slips with respect to to the scale and the right finger does not . after some distance, the left finger stops and the right one starts slipping . Then the right finger stops at a distance XR from the center (50.00 cm ) of the scale and the left one starts slopping again . This happens because to the difference in the fiictional forces on the two fingers . it the coefficients of static and dynamic between the fingers and the scale are 0.4 and 0.32 respectively , the value of XR (in cm is ...........
View SolutionOne mole of a monatomic ideal gas is taken through a cycle ABCDA as shown in the P-V diagram. Column II gives the characteristics involved in the cycle. Match them with each of the processes given in Column I.

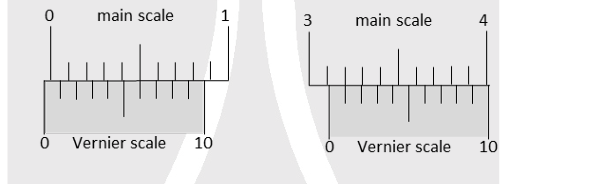
View SolutionThe smallest division on the main scale of a vernier calipers is 0.1cm. Ten divisions of the vernier scale correspond to nine divisions of the main scale. The figure below on the left shows the reading of this calipers with no gap between in two jaws. The figure on the right shows the reading with a solid sphere held between the jaws. The correct diameter of the sphere is.
View SolutionA 100W bulb has tungsten filament of total length 1.0m and radius 4×10−5m . The emissivity of the filament is 0.8 and σ=6.0×10−8Wm−2K−4 . Calculate the temperature of the filament when the bulb is operating at correct wattage.
View SolutionA body which has a surface area 5.00 cm^(2) and a temperature of 727^(@)C radiated 300 j of energy each minute. What is the emissivity of body? Steafan's constant =5.67xx10^(-8) Wm^(-2) K^(-4) .
View SolutionAn electric bulb has a solid cylindrical filament of length l and radius r and it consumes power P when connected to a power source. Another bulb having cylindrical filament of same material, operating at same voltage and emitting the same spectrum of light consumes 8 P power. find length and radius of the new filament. Assume that the filaments do not radiate from the flat ends and radiation is the only source of heat loss from the filaments.
View SolutionThe operating temperature of a tungesten filament in an indandescent lamp is 2000K and its emissivity is 0.3.
Find the surface area of the filament of a 25 watt lamp. Stefan's constant σ=5.67×10−8Wm−2K−4
View Solution20 सेमि लम्बे तथा 0.01 मिमी व्यास के टंगस्टन के तार को 2500 k ताप पर एक निर्वात बल्ब में रखा गया है। टंगस्टन का तार आदर्श कृष्णिका की अपेक्षा केवल 36 % ऊष्मा विकरित करता है। तार की विकिरण दर वाट में ज्ञात कीजिए। (स्टीफन -नियतांक=5.67×10−8 वाट/मीटर2 -K 4
View SolutionThe surface temperature of the sun is about 6000 K. the sun's radiation has maximum energy at a wavelength of 0.5 mu m. a certain light bulb filament emits radiations with a maximum at 2 mu m. if both the surface of the sun and the filament have the same emissive characteristics, then the temperature of the filament will be
View SolutionA 60 w bulb has a filament temperature of 2000 K. what will be the wattage of another bulbs of same filament area and material at a temperature of 4000 K?
View Solutionएक तापदीप्त बल्ब के टंगस्टन तंतु को विद्युत धारा के प्रवाह से उच्च तापमान पर गरम करने पर टंगस्टन तन्तु कृष्णिका विकिरण (black-body radiation) उत्सर्जित करता है। यह देखा गया है कि लम्बे समय के प्रयोग के बाद टंगस्टन तंतु में असमान वाष्पीकरण के कारण तंतु किसी भी जगह से टूट जाता है। यदि बल्ब को विद्युत शक्ति एक स्थिर वोल्टता पर दी गयी है तो निम्नलिखित में से कौनसा/कौनसे कथन सत्य है/हैं ?
View SolutionThe temperature of filament of bulb is 500 K and amount of heat radiated is E the filament is supposed to be a black body, the amount of heat radiated when the temperature of filament is 1000 K is :
View SolutionAssuming a filament in a 100W light bulb acts like a perfect blackbody, what is the temperature of the hottest portion of the filament if it has a surface area of 6.3 xx 10^(-5) m^(2) ? The Stefan-Boltzmann constant is 5.67 xx 10^(-8) W //(m^(2).K^(2)) .
View SolutionA 100W bulb has tungsten filament of total length 1.0m and raidius 4×10−5m . The emiswsivity of the filament is 0.8 and σ=6.0×10−8Wm−2K−4 . Calculate the temperature of the filament when the bulb is oprating at correct wattage.
View Solution
