In a hotel , four rooms are available , Six persons are to be accommodated in these four rooms in such a way that each of these rooms contains at least one person and at most two persons . Then the number of all possible ways in which this can be done is ______
The correct Answer is:1080
To solve the problem of accommodating 6 persons in 4 rooms such that each room has at least 1 person and at most 2 persons, we can follow these steps:
Step 1: Determine the distribution of persons in rooms
Since we have 4 rooms and need to accommodate 6 persons, the only valid distribution that satisfies the conditions (at least 1 person and at most 2 persons in each room) is:
- 2 rooms with 2 persons each
- 2 rooms with 1 person each
Step 2: Choose the rooms for 2 persons
We need to select 2 out of the 4 rooms to accommodate 2 persons. The number of ways to choose 2 rooms from 4 is given by the combination formula:
(42)=4!2!(4−2)!=4×32×1=6
Step 3: Distribute persons in the selected rooms
Now, we need to distribute the 6 persons into the rooms. We first choose 2 persons to go into the first selected room (which can hold 2 persons). The number of ways to choose 2 persons from 6 is:
(62)=6!2!(6−2)!=6×52×1=15
After placing 2 persons in the first room, we have 4 persons left. We then choose 2 persons from these 4 to go into the second selected room:
(42)=4!2!(4−2)!=4×32×1=6
Step 4: Assign the remaining persons to the other rooms
Now, we have 2 persons left, and they will each go into the remaining 2 rooms (1 person per room). The number of ways to assign these 2 persons to the 2 remaining rooms is:
2!=2
Step 5: Calculate the total arrangements
Now we can multiply all the ways together:
Total arrangements=Ways to choose rooms×Ways to choose persons for first room×Ways to choose persons for second room×Ways to assign remaining persons
=6×15×6×2
=6×15=90
90×6=540
540×2=1080
Thus, the total number of ways to accommodate the 6 persons in the 4 rooms is 1080.
Since we have 4 rooms and need to accommodate 6 persons, the only valid distribution that satisfies the conditions (at least 1 person and at most 2 persons in each room) is:
- 2 rooms with 2 persons each
- 2 rooms with 1 person each
We need to select 2 out of the 4 rooms to accommodate 2 persons. The number of ways to choose 2 rooms from 4 is given by the combination formula:
(42)=4!2!(4−2)!=4×32×1=6
Now, we need to distribute the 6 persons into the rooms. We first choose 2 persons to go into the first selected room (which can hold 2 persons). The number of ways to choose 2 persons from 6 is:
(62)=6!2!(6−2)!=6×52×1=15
(42)=4!2!(4−2)!=4×32×1=6
Now, we have 2 persons left, and they will each go into the remaining 2 rooms (1 person per room). The number of ways to assign these 2 persons to the 2 remaining rooms is:
2!=2
Now we can multiply all the ways together:
Total arrangements=Ways to choose rooms×Ways to choose persons for first room×Ways to choose persons for second room×Ways to assign remaining persons
=6×15×6×2
=6×15=90
90×6=540
540×2=1080
Topper's Solved these Questions
Similar Questions
45 In a hotel four rooms available. Six persons are to be accommodated in these four rooms in such a way that each of these rooms contains at least one person and at most two persons. Then the number of all possible ways in which this can be done is 'P'. Then sum of digits of 'P' is equal to
View SolutionFind the number of ways in which four persons can sit on six chairs.
View Solution
Knowledge Check
Six X have to be placed in the squares of Fig. 6.6 such that each row contain at least one X. The number of ways in which this can be done is
 A25B26C27D30
A25B26C27D305 different objects are to be distributed among 3 persons such that no two persons get the same number of objects. Number of ways this can be done is,
A60B90C120D150
Six X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:
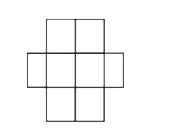
View SolutionSix X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:

View SolutionFour persons entered the lift cabin on the ground floor of a six floor office . if the 4 persons can leave the cabin at any one of the 5 floors , then find the number of ways in which this can be done
View SolutionEight people enter an elevator. At each of four floors atleast one person leaves the elevator after which elevator is empty. The number of ways in which this is possible is :
View SolutionIn a three-storey building, there are four rooms on the ground floor, two on the first and two on the second floor. If the rooms are to be allotted to six persons, one person occupying one room only, the number of ways in which this can be done so that no floor remains empty is a. 8P6−2(6!) b. 8P6 c. 8P5(6!) d. none of these
View SolutionThere are eight rooms on the first floor of a hotel, with four rooms on each side of the corridor, symmetrical situated (that is each room is exactly opposite to one other room). Four guests have to be accommodation In four of the eight rooms (that is, one in each) such that no two guests are in adjacent rooms or in opposite rooms. If N is the number of ways in which guests can be accommodated. Then the value of N6 is
View Solution
