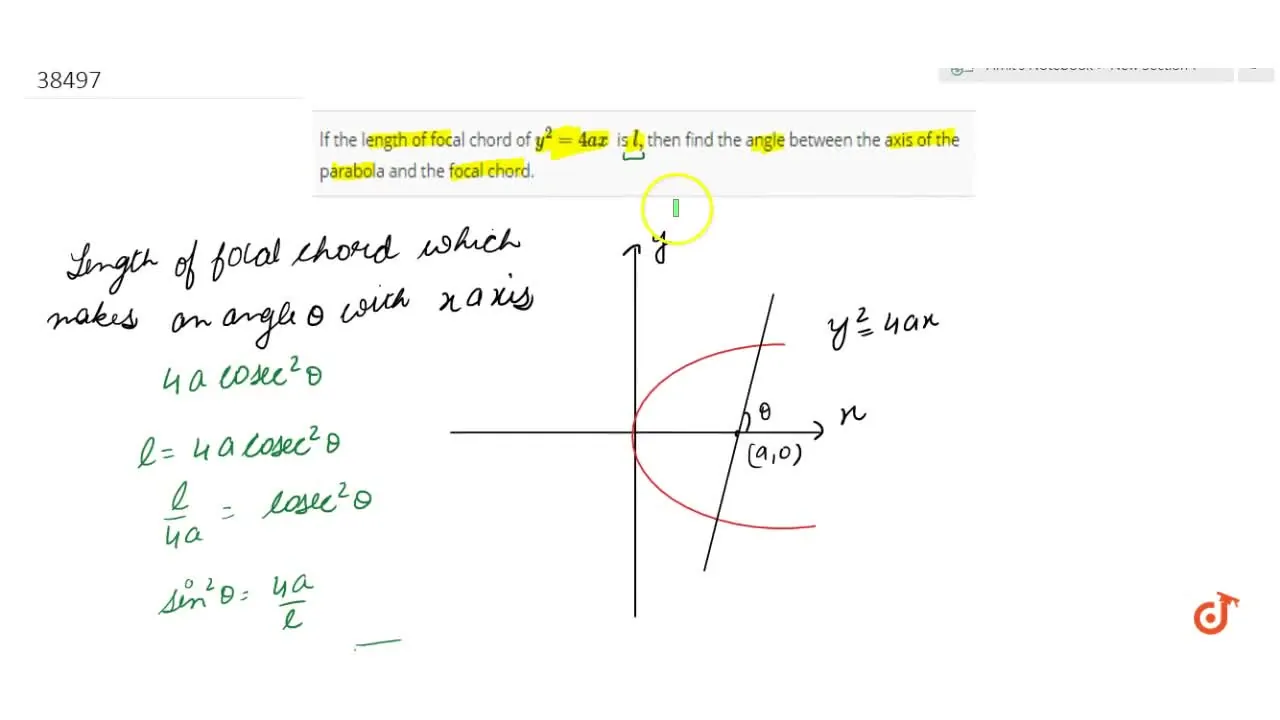
If the length of focal chord of y^2=4a x is l , then find the angle be

If the lsope of the focal chord of $y^{2} = 16 x$ is 2, then the length of the chord, is
A22
B24
C20
D18
If the length of a focal chord of parabola $y^{=} 4 x$ is $\frac{25}{4}$ and has a positive slope, then the slope of the focal chord will be
A $\sqrt{3}$
B $\frac{1}{\sqrt{3}}$
C $\frac{4}{3}$
D1
Let one end of focal chord of parabola $y^{2} = 8 x$ is $(\frac{1}{2}, - 2)$ , then equation of tangent at other end of this focal chord is
A $x + 2 y + 8 = 0$
B $x + 2 y = 8$
C $x - 2 y = 8$
D $x - 2 y + 8 = 0$

If the length of focal chord of $y^{2} = 4 a x$ is $l,$ then find the angle between the axis of the parabola and the focal chord.