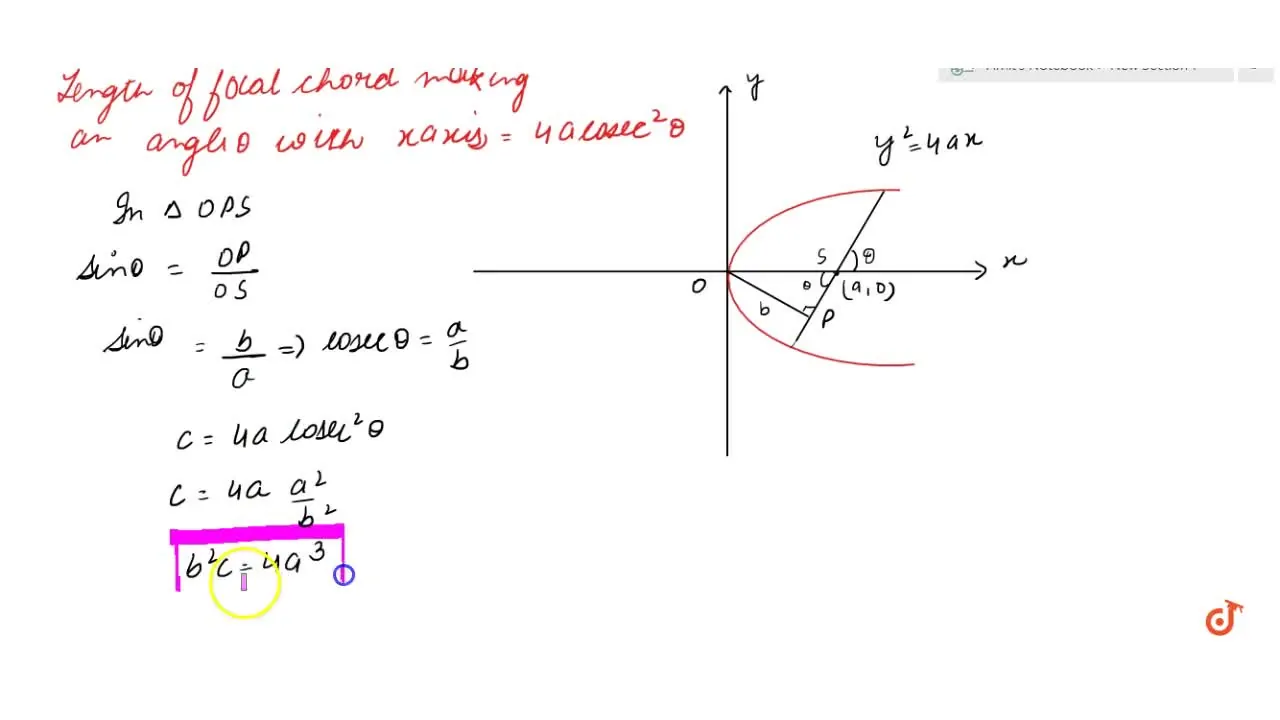
If the length of a focal chord of the parabola $y^{2} = 4 a x$ at $a$ distance $b$ from the vertex is $c,$ then prove that $b^{2} c = 4 a^{3} \dot{}$

Video Solution

Answer

Step by step video & image solution for If the length of a focal chord of the parabola y^2=4a x at a distance b from the vertex is c , then prove that b^2c=4a^3dot by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 MATHS PARABOLA

Knowledge Check

Question 1 - Select One
The length of a focal chord of the parabola $y^{2} = 4 a x$ at a distance b from the vertex is c. Then
A $a^{2} = b c$
B $a^{3} = b^{2} c$
C $b^{2} = a c$
D $b^{2} c = 4 a^{3}$
Question 2 - Select One
The length of the focal chord of the parabola $y^{2} = 4 x$ at a distance of 0.4 units from the origin is
A22 units
B23 units
C24 units
D25 units
Question 3 - Select One
If a focal chord of the parabola be at a distanced from the vertex, then its length is equal to
A $\frac{2 a^{2}}{d}$
B $\frac{a^{2}}{d^{2}}$
C $\frac{4 a^{3}}{d^{2}}$
D $\frac{d^{2}}{a}$

If the length of a focal chord of the parabola $y^{2} = 4 a x$ at $a$ distance $b$ from the vertex is $c,$ then prove that $b^{2} c = 4 a^{3} \dot{}$

Similar Questions

Knowledge Check

The length of a focal chord of the parabola $y^{2} = 4 a x$ at a distance b from the vertex is c. Then

The length of the focal chord of the parabola $y^{2} = 4 x$ at a distance of 0.4 units from the origin is

If a focal chord of the parabola be at a distanced from the vertex, then its length is equal to

Recommended Questions

If the length of a focal chord of the parabola y 2 = 4 a x at a distance b from the vertex is c , then prove that b 2 c = 4 a 3 .

Similar Questions

Knowledge Check

The length of a focal chord of the parabola y2=4ax at a distance b from the vertex is c. Then

The length of the focal chord of the parabola y2=4x at a distance of 0.4 units from the origin is

If a focal chord of the parabola be at a distanced from the vertex, then its length is equal to

Recommended Questions

If the length of a focal chord of the parabola $y^{2} = 4 a x$ at $a$ distance $b$ from the vertex is $c,$ then prove that $b^{2} c = 4 a^{3} \dot{}$

The length of a focal chord of the parabola $y^{2} = 4 a x$ at a distance b from the vertex is c. Then

The length of the focal chord of the parabola $y^{2} = 4 x$ at a distance of 0.4 units from the origin is