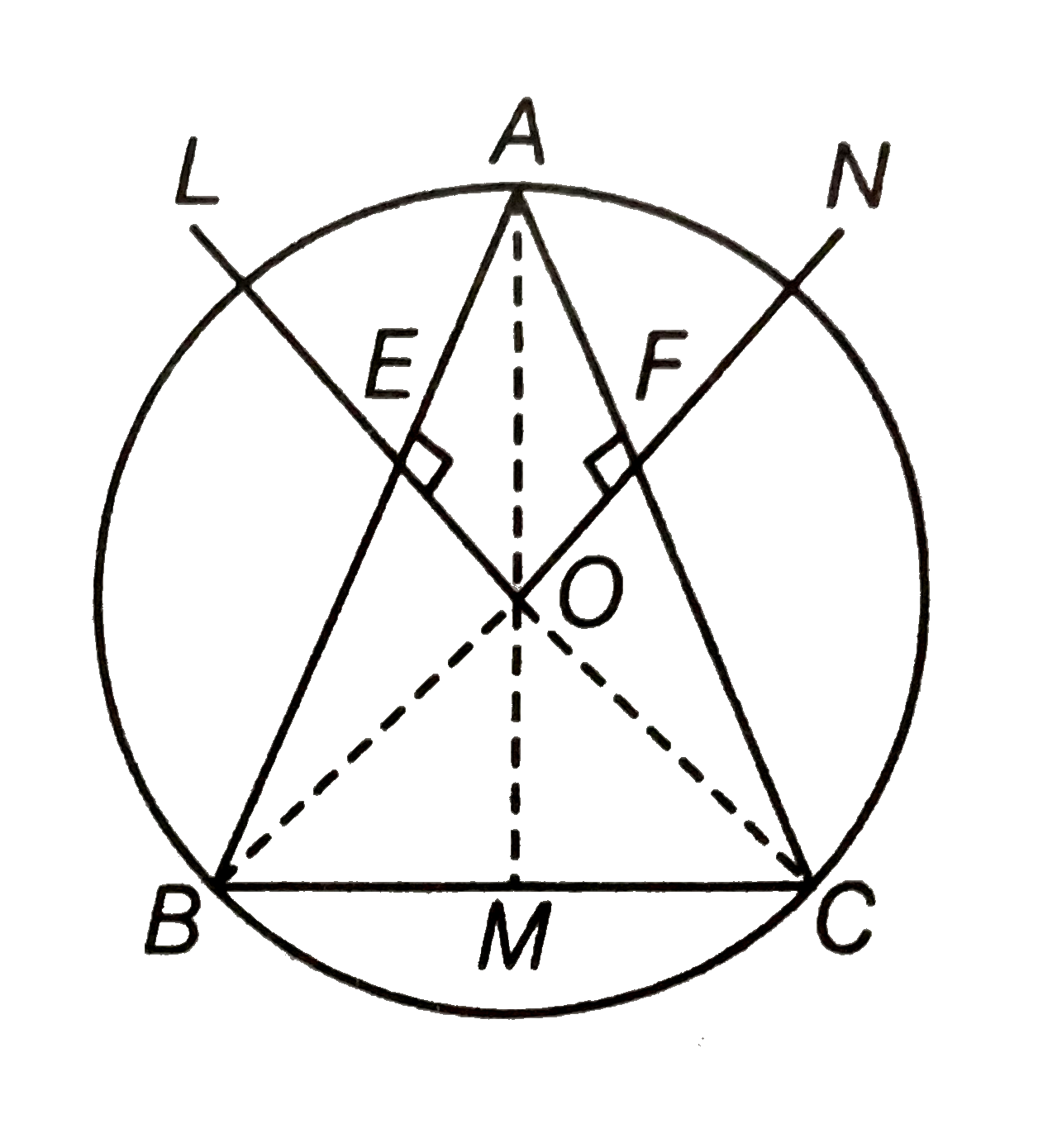
From a point O inside a triangle ABC, perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB, respectively. Prove that the perpendiculars from A, B and C to the sides EF, FD and DE are concurrent
Let the position vectors of points A,B,C,D,E and F be w.r.t O. Let perpendiculars from A to EF and from B to DF meet each other at H. let position vectors of H be . We join CH. In order to prove the statement given in the question. it is sufficient it is sufficient to prove that CH is prependicular to DE.
Now
as
Also
Adding (iv) and (v) , we get
[ using (i), (ii) and (iii))]
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGEChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Exercise
Explore 337 Videos
- DETERMINANTSBook:CENGAGEChapter:DETERMINANTSExercise:Question Bank
Explore 23 Videos
- DIFFERENTIAL EQUATIONSBook:CENGAGEChapter:DIFFERENTIAL EQUATIONSExercise:Question Bank
Explore 25 Videos
Similar Questions
From a point O inside a triangle ABC, perpendiculars OD,OEandOf are drawn to rthe sides BC,CAandAB, respecrtively. Prove that the perpendiculars from A,B,andC to the sides EF,FDandDE are concurrent.
View SolutionA, B and C are three points on a circle. Prove that the perpendicular bisectors of AB, BC and CA are concurrent.
View Solution
Knowledge Check
From a point O in the interior of a DeltaABC perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
AAF2+BD2+CE2=AE2+CD2+BF2BAB2+BC2=AC2CAF2+BD2+CE2=OA2+OB2+OC2DAF2+BD2+CE2=OD2+OE2+OF2From a point O in the interior of a ΔABC perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively, then which one of the following is true ?
AAF2+BD2+CE2=AE2+CD2+BF2BAB2+BC2=AC2CAF2+BD2+CE2=OA2+OB2+OC2DAF2+BD2+CE2=OD2+OE2+OF2In a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector →AD is equal to
A→BE+→CFB→BE−→CFC→CF−→BED−→BE−→CF
From a point P inside the triangle ABC, perpendicular PQ, PR and PS are respectively drawn to sides BC, CA and AB.
Prove that AS2+BQ2+CR2=BS2+CQ2+AR2
View SolutionProve that the perpendicular let fall from the vertices of a triangle to the opposite sides are concurrent.
View SolutionIn ΔABC,ADandBE are perpendiculars from A and B to the sides BC and AC, then
View SolutionLet →a,→b,→c form sides BC,CA and AB respectively of a triangle ABC then
View SolutionIn a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
View Solution

