OABC is regular tetrahedron in which D is the circumcentre of OAB and E is the midpoint of edge AC. Prove that DE is equal to half the edge of tetrahedron.
Let −−→OA=→aand−−→OB=→b
since △ABC is equilateral, the circumecenters, triangle coincide with the centroid, therefore,
−−→OD=→a+→b3
Also−−→OE=→a+→c2
−−→DE=→a=3→c−2→b6
∣∣∣−−→DE∣∣∣2=∣∣∣→a+3→c−2→b6∣∣∣2
Since, |→a|=∣∣→b∣∣=|→c|andθ=60∘ we have,
∣∣∣−−→DE∣∣∣2=136(a2+9a2+4a2+6a22−12a22−4a22)
a24
or ∣∣∣−−→DE∣∣∣=a2

Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Book:CENGAGEChapter:DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS Exercise:Exercise
Explore 337 Videos
- DETERMINANTSBook:CENGAGEChapter:DETERMINANTSExercise:Question Bank
Explore 23 Videos
- DIFFERENTIAL EQUATIONSBook:CENGAGEChapter:DIFFERENTIAL EQUATIONSExercise:Question Bank
Explore 25 Videos
Similar Questions
OABC is regular tetrahedron in which D is the circumcentre of OAB and E is the midpoint of edge AC. Prove that DE is equal to half the edge of tetrahedron.
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14areaof△ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionABC is a triangle. D is a point on AB such that AD=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC.
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionIn Figure, AD is the median and DE∣∣AB . Prove that BE is the median.
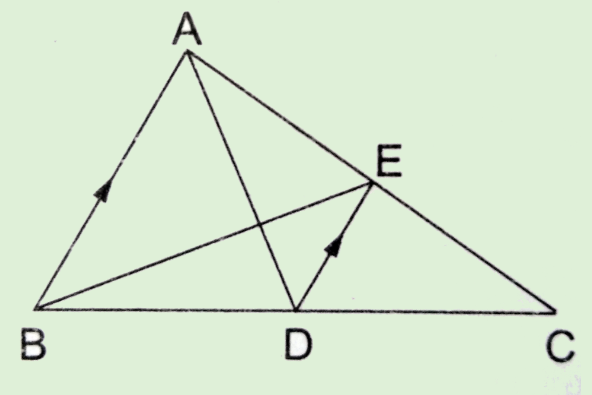
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionIF OABC is a tetrahedron where O is the origin and A,B and C have respective positions vectors as ¯a,¯band¯c then prove that the circumcentre of the tetrahedron is (¯a)2(¯bׯc)+(¯b)2(¯cׯa)+(¯c)2(¯aׯb)2[¯a¯b¯c]
View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB≅ADC
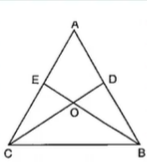
View SolutionOABC is a tetrahedron D and E are the mid points of the edges −−→OA and −−→BC. Then the vector −−→DE in terms of −−→OA,−−→OBand−−→OC
View SolutionRegular tetrahedron a tetrahedron whose all the edges are of equal length is called a regular tetrahedron.
View Solution

