Question

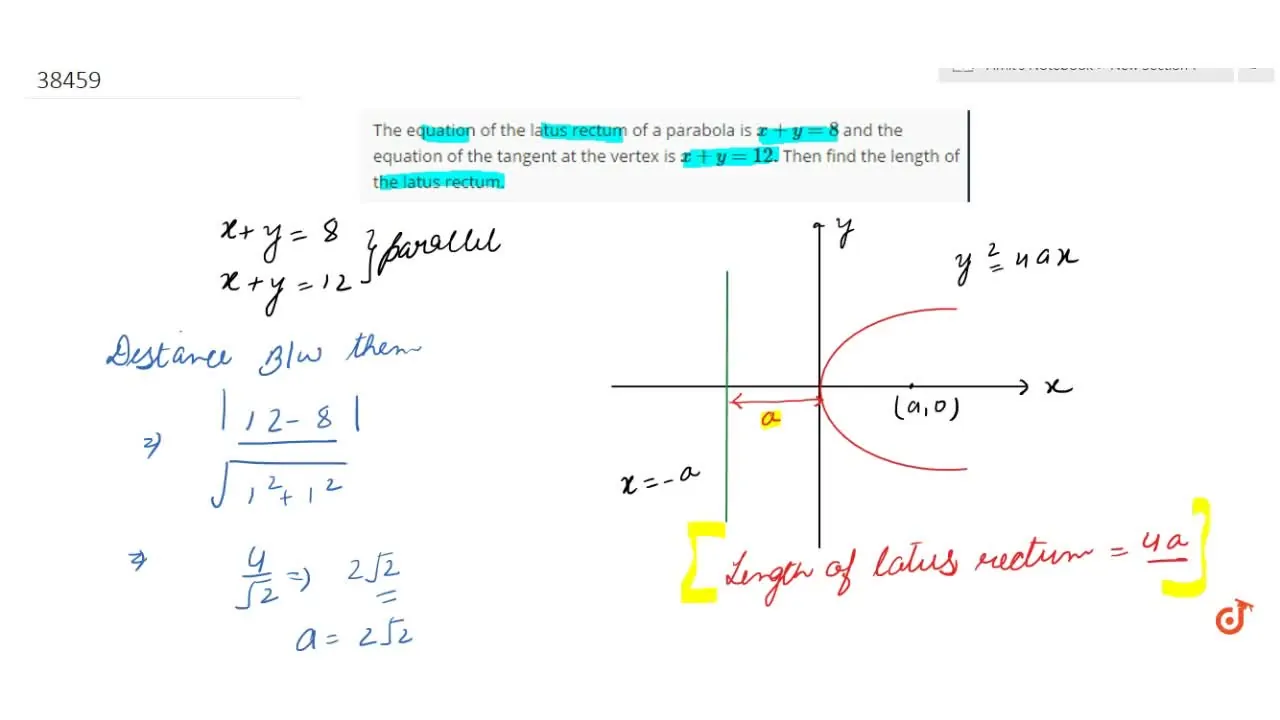
The equation of the latus rectum of a parabola is $x+y=8$
and the equation of the tangent at the vertex is $x+y=12.$
Then find the length of the latus rectum.

Answer

`8sqrt(2)`

Explanation

Since the equation of latus rectum and the equation of tangent both are parallel, and the distance them is one - fourth of the latus rectum, the distance between them is
`a=|(-8+12)/(sqrt(1^(2)+1^(2)))|=(4)/(sqrt(2))=2sqrt(2)`
`:." Length of latus rectum"=4a=4(2sqrt(2))=8sqrt(2)`