Question

Explain the Maxwell's modification of Ampere's circuital law.

Explanation

(i) The electric current passing through the wire is the conduction current . This current generates magnetic field around the wire connected across the capacitor.
(ii) "Therefore, when a magnetic needle is kept near the wire, deflection is observed. In order to compute the strength of magnetic field at a point, we use Ampere.s circuital law is used which states that .the line integral of the magnetic field `vecB` around any closed loop is equal to po times the net current I threading through the area enclosed by the loop. Ampere.s law in equation form is
`ointvecB*vecl=mu_0 I(t)" ...(1)"`
(iii) where H, is the permeability of free space

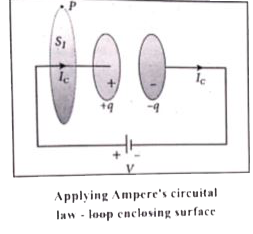
To calculate the magnetic field at a point P near the wire an amperian loop (circular loop) which encloses the surfaces `S_1`, (circular surface), using (equation (1)),
`ointvecB*vec(dl)=mu_0 I_(C)" ...(2)"`
(iv) Suppose the same loop is enclosed by balloon shaped surface `S_2`.. This means that the boundaries of two surfaces `S_1`, and `S_2`, are same but shape of the enclosing surfaces are different (first surface (`S_1`) is circular in shape and second one is balloon shaped surface (`S_2`,)). As the Ampere.s law does not depend on shape of the enclosing surface, the integrals will give the same answer. But by applying (equation (1)),
`underset("enclosing"S_2)(oint)vecB*vec(dl)=0" ...(3)"`
By applying equation (1)
`ointvecB*vec(dl)=0"enclosing "s_2`

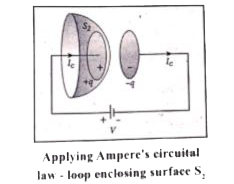
(v) The right hand side of equation is zero because the surface `S_2`, no where touches the wire carrying conduction current and further, there is no current in between the plates of the capacitor (there is a discontinuity). So the magnetic field at a point P is zero.
(vi) Due to external sauce (battery or cell), the capacitor gets charged up because of current flowing through the capacitor. This produces an increasing electric field between the capacitor plates. The time varying electric flux between the plates of the capacitor produces a current known as displacement current.

(vii) From Gauss.s law
`phi_E = ointointvecE.dvecA = EA = q/epsi_0`
Where A is the area of the plates of capacitor.
The change in electric flux is
`(dphi_E)/(dt) = 1/epsi_0 (dq)/(dt) rArr(dq)/(dt) = I_d = epsi_d (dphi_E)/(dt)`
where `I_d` is know as displacement current.
(viii) The displacement current can be defined as the current in the region in which the electric field and the electric flux are changing with time. i.e whenever the change in electric field, displacement current is produced. Maxwell modified Ampere.s law as
`oint vecB.d vecS = mu_0 ( I_c +I_d)" ...(4)"`
where `I = 1_c + I_d` which means the total current enclosed by the surface is sum of conduction current and displacement current.
(ix) When a constant current is applied, displacement current `I_d`, = 0 and hence `I_c` = I. Between the plates, the conduction current `I_c` = 0 and hence `I_d` = I.