Derive the expression for the radius of the orbit of the electron and its velocity using Bohr atom model. Solution in Tamil
(i) Consider an atom which contains the nucleus at rest and an electron revolving around the nucleus in a circular orbit of radius rn. as shown in Figure.
(ii) Nucleus is made up of protons and neutrons. Since proton is positively charged and neutron is electrically neutral, the charge of a nucleus is purely the total charge of protons.
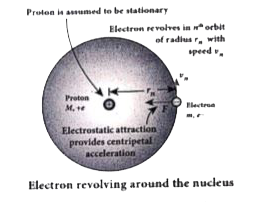
(iii) Let Z be the atomic number of the atom, then +Ze is the charge of the nucleus. Let -e be the charge of the electron. From Coulomb.s law, the force of attraction between the nucleus and the electron is
→Fcoloumb=14πε0(+Z3)(−e)r2n
=−14πε0Ze2r2nˆr
(iv) This force provides necessary centripetal force →Fcentripetal=mv2nrnˆr
(v) where m be the mass of the electron that moves with a velocity vn, in a circular orbit. Therefore,
∣∣→Fcoloumb∣∣=∣∣→Fcentripetal∣∣
14πε0Ze2r2n=mv2mrn,
rn=4πε0(mvnrn)2Zme2
From Bohr.s ssumption, the angular momentum quantization condition
mvnrn=nh
∴ rn=4πε0(mvnrn)2Zme2
rn=4πε0(nh)2Zme2=4πε0n2h2Zme2
rn=(ε0h2πme2)n2Z (∴h=h2π)
Where n∈N. Since, ε0, h, e and π are constants. Therefore, the radius of the orbit becomes
rn=a0n2Z
where a0=ε0h2πme2=0.529.
Similar Questions
Derive an expression for the radius of nth Bohr's orbit of hydrogen atom hence write the expression for the radius of first orbit of hydrogen atom.
View SolutionUsing Bohr's postulates of the atomic model, derive the expression for radius of th electron orbit. Thus, obtain the expression of Bohr's radius.
View SolutionUsing Bohr's postulates of the atomic model. Derive the expression for radius of nth electron orbit, thus obtaining the expression for Bohr's radius.
View SolutionThe electric current I created by the electron in the ground state of H atom bohr model in terms of bohr radius (a0) and velocity of electron in first orbit v0 is
View SolutionState Bohr’s postulates for atomic model and derive an expression for radius of the electron in an orbit.
View SolutionUsing Bohr's atomic model, derive an equation of the radius of the nth orbit of an electron.
View SolutionWrite the formula for the orbital radius of the electron in the atom based on the Bohr atomic model.
View SolutionBohr's atomic model || Radius OF electron in nth Bohr orbit || Velocity,time period & frequency OF electron in nth bohr orbit
View Solution
