Define : (i) collinear vectors and (ii) coplanar vectors. Solution in Bengali
Step by step video & image solution for Define : (i) collinear vectors and (ii) coplanar vectors. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTORBook:CHHAYA PUBLICATIONChapter:VECTORExercise:Higher Order Thinking Skill (Hots) Questions
Explore 28 Videos
- VECTORBook:CHHAYA PUBLICATIONChapter:VECTORExercise:EXERCISE (Multiple Choice Questions)
Explore 44 Videos
- VECTORBook:CHHAYA PUBLICATIONChapter:VECTORExercise:CBSE SCANNER
Explore 19 Videos
- THERMOMETRYBook:CHHAYA PUBLICATIONChapter:THERMOMETRYExercise:EXAMINATION ARCHIEVE - WBJEE
Explore 1 Video
- VISCOSITY AND SURFACE TENSIONBook:CHHAYA PUBLICATIONChapter:VISCOSITY AND SURFACE TENSIONExercise:EXERCISE (CBSE SCANNER)
Explore 9 Videos
Similar Questions
Under which condition will the magnitude of scalar sum be equal to the magnitude of vector sum ?
View SolutionWhat is the condition for →A+→B=→A−→B to be valid ?
View SolutionA body is projected horizontally from the top of a building of height h. Velocity of projection is u. Find
View SolutionA scientist proposes a new temperature scale in which the ice point is 25X (X is the new unit of temperature) and the steam point is 305X. The specific heat capacity of water in this new scale is (in J⋅kg−1⋅X−1)
View SolutionState and prove Bernoulli's theorem.
View SolutionAnswer the following as true or false.
(i) →aand −→aare collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude
View SolutionExplain (i) Unit vector (ii) Equal vectors (iii) Negative vectors, (iv) Coinitial v ectors (v) Collinear vectors and (vi) Copanar vectors.
View SolutionA vector coplanar with the non-collinear vectors ¯aand¯b is
View SolutionDefine Coinitial vector and Collinear vector .
View SolutionI : The three points with position vectors i - 2j + 3k, 2i + 3j - 4k and -7j + 10k are collinear.
II : The vectors a - 2b + 3c, 2a + 3b - 4c, -7b + 10c are coplanar.
View SolutionI : Two non-zero, non-collinear vectors are linearly independent.
II : Any three coplanar vectors are linearly dependent. which one is true?
View SolutionDefine collinear vectors.
View SolutionIn the figure, which of the vectors are
(i) Collinear vectors
(ii) Equal vectors
(iii) Cointial vectors
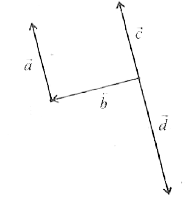
View SolutionIn the figure which vectors are
(i) equal (ii) collinear (iii) coinitial
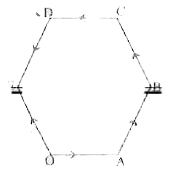
View SolutionIn Fig 10.5 ., which of the vectors are :
(i) Collinear
(ii) Equal
(iii) Coinitial
View Solution

