A gas expands with temperature according to the relation, V=kT2/3 where k is a constant Word done when the temperature changes by 60 K is (R= Universal gas constant).Solution in Telugu
10 R
20 R
50 R
40 R
Given, V=kT2/3
From definition of word done,
dW=PdV=RTVdV
=RTkT2/3dV.....(i)
Now V=kT2/3
Taking derivative on the both sides, we get
dV=K23T1/3dT.......(ii)
Subsituting the value of Eqs. (ii) in Eqs. (i) and taking integration on the both sides, we get
W=23R∫T2T1dT=23R(T2−T1)
=23R(60−0)=23×R×60=40R
Topper's Solved these Questions
- AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED)Book:TS EAMCET PREVIOUS YEAR PAPERSChapter:AP EAMCET ENGINEERING ENTRANCE EXAM ONLINE QUESTION PAPER 2019 (SOLVED)Exercise:Physics
Explore 40 Videos
- AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)Book:TS EAMCET PREVIOUS YEAR PAPERSChapter:AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)Exercise:Physics
Explore 40 Videos
Similar Questions
N divisions on the main scale of a vernier calipers coincide with (N +1) division of the vernier scale. If each division of main scale is a units, then the least count of the calipers is :
View SolutionA monoatomic ideal gas through a cyclic process as shown in the figure . The efficiency of this process is
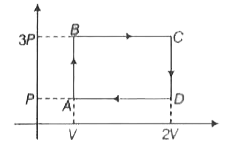
View SolutionOne mole of a gas expands with temperature T such thaht its volume, V=KT2, where K is a constant. If the temperature of the gas changes by 60∘C then the work done by the gas is 120R
View SolutionA gas expands with temperature according to the relation V=KT^(2/3) .Work done when the temperature changes by 60K is.
View SolutionOne mole of a gas expands such that its volume 'V' changes with absolute temperature 'T' in accordance with the relation V=KT2 where 'K' is a constant. If the temperature of the gas changes by 60∘C, then work done by the gas (R is universal gas constant)
View SolutionIn a thermodynamic process two moles of a monatomic ideal gas obeys PV–2=constant. If temperature of the gas increases from 300 K to 400 K, then find work done by the gas (Where R = universal gas constant)
View SolutionOne mole of a gas expands such that its volume 'v' changes with absolute temperature 'T' in accordance with the ralation V = HT^(2) where 'K' is a constant . If the temperature of the gas changes by 60^(@) C , then work done by the gas is (R is universal gas constant ) .
View SolutionA gas expands with temperature according to the relation V = KT^(2//3) where K is a constant. The work done by the gas when the temperature changes by 60 K is
View SolutionThe volume of one mole of an ideal gas changes from V to 2V at temperature 300 K. If R is universal gas constant, then work done in this process is
View Solutionएक गैस का ताप V=RT2/3 सम्बन्ध के अनुसार बढ़ता है। जब ताप 60 K तक परिवर्तित हो जाता है, तब कृत कार्य होगा
View SolutionA gas expands with temperature according to the relation V=KT23.Work done when the temperature changes by 60K is.
View SolutionThe volume V of a given mass of monoatomic gas changes with temperature T according to the relation V=KT2/3. The workdone when temperature changes by 90 K will be xR. The value of x is [R = universal gas constant]
View SolutionA gas expands with temperature according to the relation V = kT^(2//3) . What is the work done when the temperature changes by 30^(@)C ?
View Solutionऊष्मागतिक प्रक्रम में, एक आदर्श एकपरमाण्विक गैस के एक मोल का ताप और आयतन VT = k संबंध के अनुसार परिवर्तित होता है, जहाँ k एक धनात्मक स्थिरांक है। इस प्रक्रम में, यदि गैस का ताप, ΔT से बढ़ जाता है, तब गैस द्वारा अवशोषित ऊष्मा की मात्रा कितनी है? [R सार्वत्रिक गैस नियतांक है]
View SolutionIn a thermodynamic process two moles of a monatomic ideal gas obeys PV–2=constant. If temperature of the gas increases from 300 K to 400 K, then find work done by the gas (Where R = universal gas constant)
View Solution

