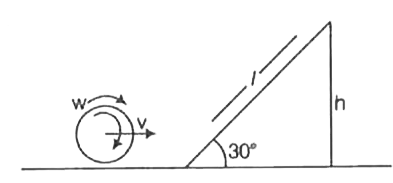
A solid sphere is projected up along an inclined plane of inclination $30^{\circ}$ with the horizontal with a speed of $4 m s^{- 1}$ . If it rolls without slipping , the maximum distance traversed by it is . .. . . . $(g = 10 m s^{- 2})$ Solution in Telugu

A

$2.24 m$

B

112 m

C

1 . 12 m

D

22.4 m

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Given, v = $4 m s^{- 1} A l s o v = r ω$
Hence,
KE at bottom
$= K_{transletion} + K_{rotation}$
$= \frac{1}{2} m v^{2} + \frac{1}{2} I ω^{2}$
$= \frac{1}{2} m v^{2} + \frac{1}{2} [\frac{2}{5} m r^{2} \frac{v^{2}}{r^{2}}]$
$= \frac{1}{2} m v^{2} + \frac{1}{2} \times \frac{2}{5} m v^{2}$
$= \frac{1}{2} (\frac{7}{5} m v^{2})$
At hight h, energy conservation gives
$\frac{1}{2} (\frac{7}{5}) m v^{2} = m g h$
$\Rightarrow h = \frac{7}{10} \times \frac{v^{2}}{g}$
$= \frac{7}{10} \times \frac{16}{10}$
= 1 . 12m
As, $l = h / {sin 30}^{\circ}$
$\Rightarrow l = 2 \times h$
= 224 m

Updated on:21/07/2023

|

Class 12 PHYSICS AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)

Topper's Solved these Questions

Similar Questions

TS EAMCET PREVIOUS YEAR PAPERS-AP EAMCET ENGINEERING ENTRANCE EXAM QUESTION PAPER 2017 (SOLVED)-Physics

Home
Ask Doubt
Profile