Question

(a) किसी गोले का , इसके किसी व्यास के परित जड़त्व आघूर्ण $2M{R}^2/5$ है जहाँ M गोले का द्रव्यमान एवं R इसकी त्रिज्या है । गोले पर खींची गई स्पर्श रेखा की परित इसका जड़त्व आघूर्ण ज्ञात कीजिए ।
(b) M द्रव्यमान एवं R त्रिज्या वाली किसी डिस्क का इसके किसी व्यास के प्रीत जड़त्व आघूर्ण $M{R}^2/4$ है । डिस्क के लंबवत इसकी और से गुजरने वाली अक्ष के परित इस चकती का जड़त्व आघूर्ण ज्ञात कीजिए ।

Explanation

(a) माना R त्रिज्या तथा M द्रव्यमान के गोले के व्यास के परित उसका आघूर्ण `I_(AB)` है
`:. I_(AB) = (2)/(5) MR^(2)`
यहाँ पर गोला ठोस है ।

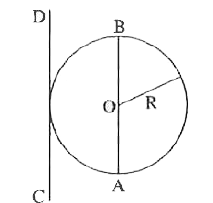
माना गोले के व्यास AB के समांतर स्पर्शज्या CD है और दोनों समांतर अक्षों के बीच की दूरी R है । यदि CD अक्ष के परित इसका जड़त्व आघूर्ण `I_(CD)` है समांतर अक्ष प्रमेय से ,
`I_(CD) = I_(AB) + MR^(2) = (2)/(5) MR^(2) + MR^(2)`
`I_(CD) = (7)/(5) MR^(2)`
(b) डिस्क का व्यास के परित जड़त्व आघूर्ण `= (MR^(2))/(4)` इसलिए चकती के केंद्र से गुजरने वाली व तल के लंबवत अक्ष के सापेक्ष जड़त्व आघूर्ण
`I_(z) + I_(x) + I_(y)`
लम्ब अक्ष प्रमेय से ,
`:.` दोनों व्यास समान है ।
`:. I_(x) = I_(y)`
`I_(z) = I_(x) + I_(x) = 2I_(x)`
`I_(z) = 2 xx (MR^(2))/(4) = (MR^(2))/(2)`
`:.` डिस्क के लंबवत कोर से गुजरने वाली अक्ष के परित चकती का जड़त्व आघुर्णन (समांतर अक्षों की प्रमेय से )
`I_(z) = I_(z) + MR^(2)`
`= (1)/(2) MR^(2) + MR^(2)`
`I_(z) = (3)/(2) MR^(2)`