In a triangle locate a point in its interior which is equidistant from all the sides of the triangle.
Video Solution
Text Solution
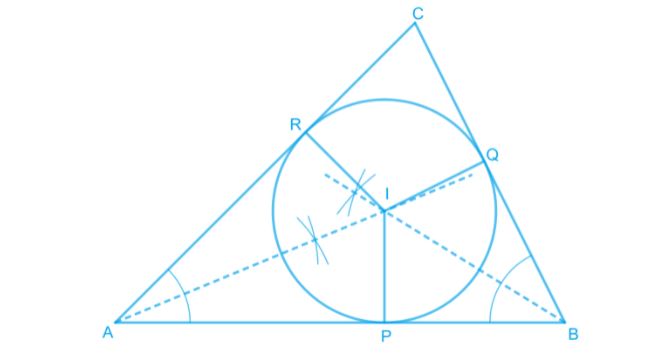
Here, in ∆ABC, we can find the incentre of this triangle by drawing the angle bisectors of the interior angles of this triangle. I is the point where these angle bisectors are intersecting each other.
Therefore, I is the point which is equidistant from all the sides of ΔABC that is IP=IQ=IP.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the number of points in the plane of a triangle ABC which are at equal distance from the vertices of the triangle ?
A0B1C2D3The point in the plane of a triangle which is at equal perpendicular distance from the sides of the triangle is :
AcentroidBincentreCcircumcentreDorthocentreThe coordinates of the point which is equidistant from the three vertices of the △AOB as shown in the figure is
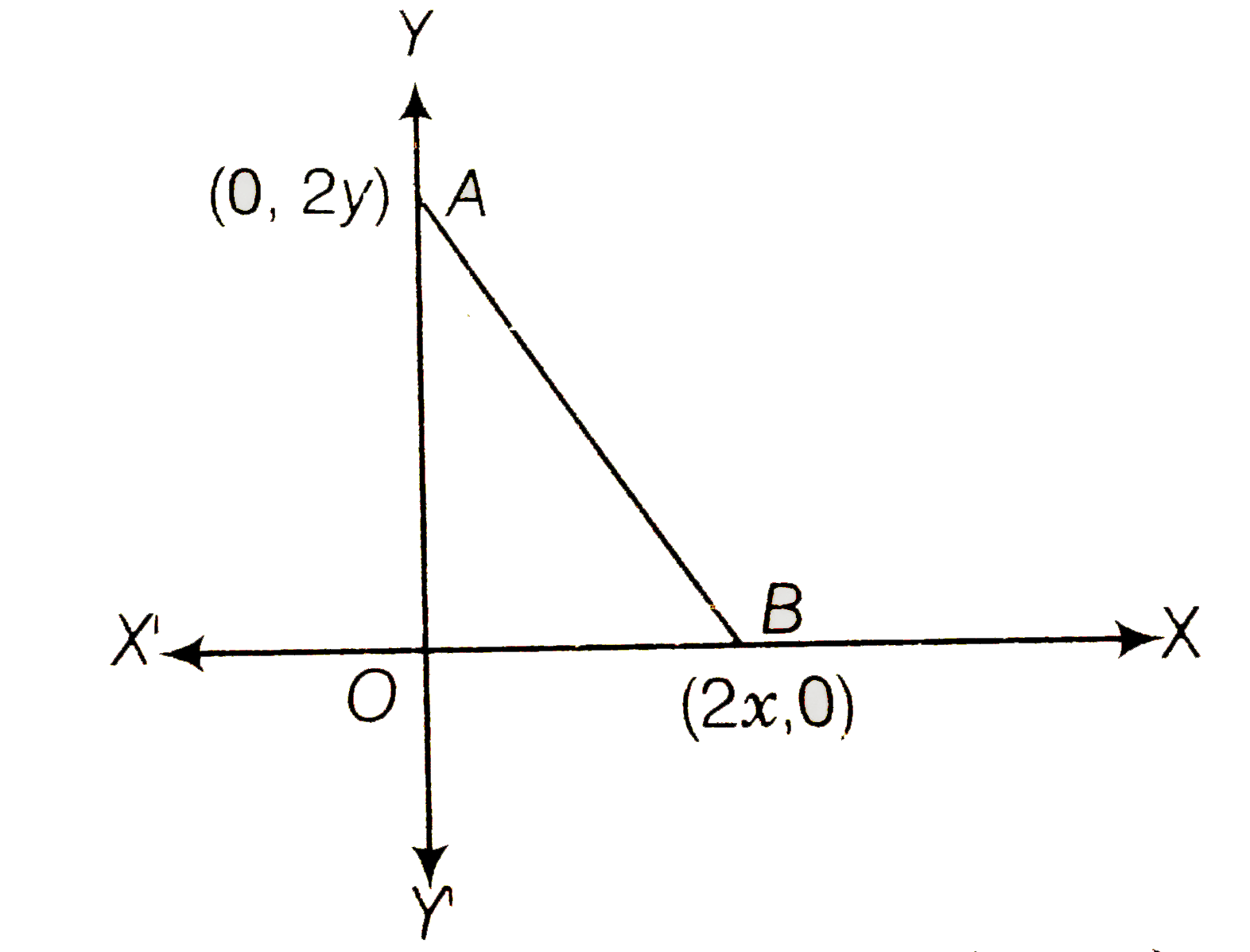 A(x,y)B(y,x)C(x2,y2)D(y2,x2)
A(x,y)B(y,x)C(x2,y2)D(y2,x2)
Find the locus of the point which is equidistant from the sides AB and AC of triangle ABC.
View SolutionThree charges of 1 nC, 2 nC and 3 nC are placed at the corners of an equilateral triangle of side √3m. Calculate electrostatic potential at a point equidistant from the three corners of the triangle.
View SolutionIncentre of a triangle lies in the interior of :
View SolutionIncentre of a triangle lies in the interior of :
View SolutionThe loucs of the point which is equidistant from the three determined by the sides of a triangles is _______
View Solution