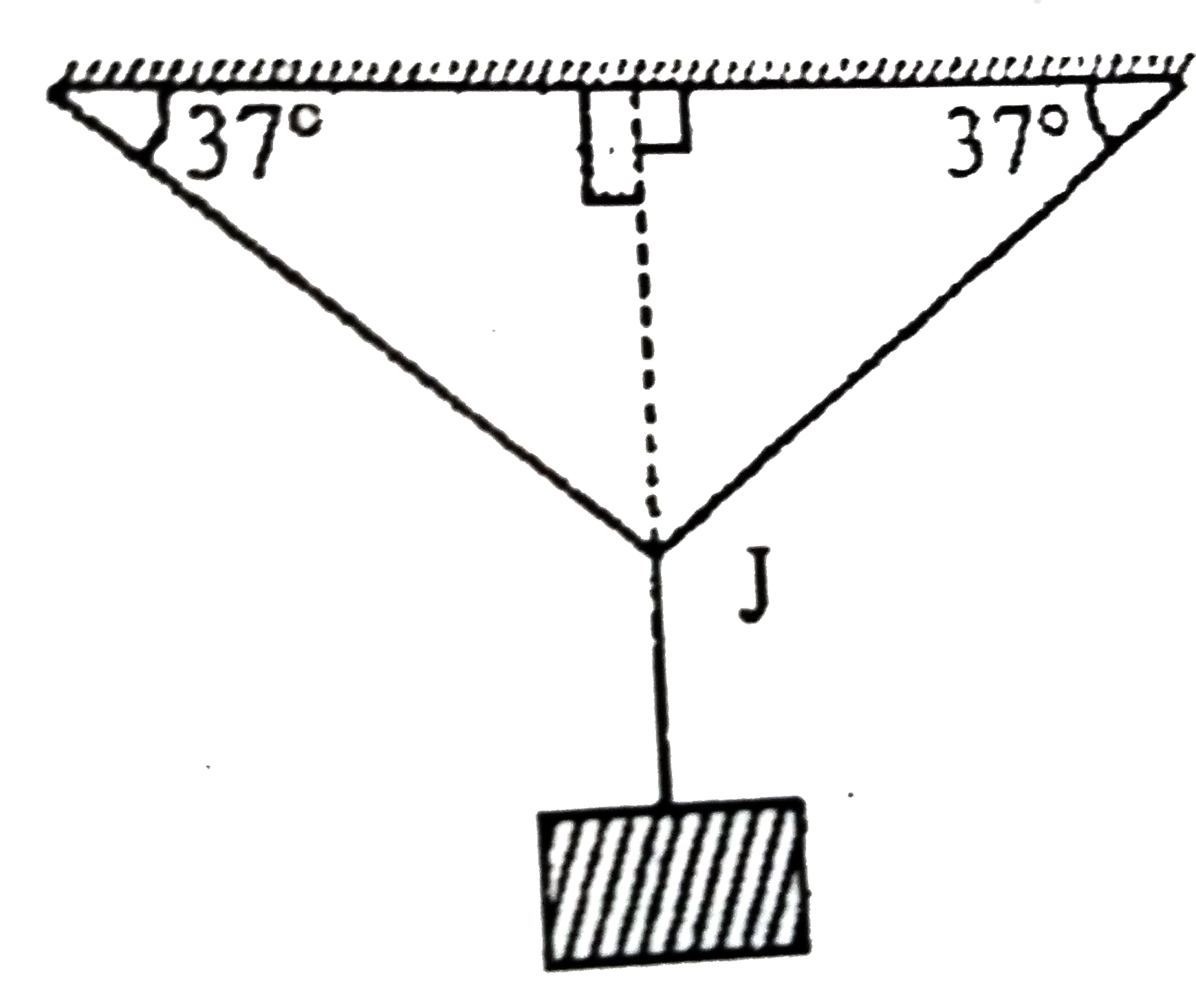
A block is hanged by means of two identical wires having cross section

A uniform rod of cross-section $4 m m^{2}$ is heated from $0^{\circ} C to 10^{\circ} C .$ The coefficient of linear expansion of the rod, $\propto = 12 \times 10^{- 6} /^{\circ} C$ and Young's modulus $= 10^{11} N / m^{2} .$ The strain produced in the rod is
A $8 \times 10^{- 4}$
B $12 \times 10^{- 4}$
C $8 \times 10^{- 5}$
D $12 \times 10^{- 5}$
A steel wire of length 20 cm and uniform cross-section $1 m m^{2}$ is tied rigidly at both the ends. If the temperature of the wire is altered from $40^{\circ} C$ to $20^{\circ} C$ , the change in tension. [Given coefficient of linear expansion of steel is $1.1 \times 10^{5} .^{\circ} C^{- 1}$ and Young's modulus for steel is $2.0 \times 10^{11} N m^{- 2}$ ]
A22 N
B44 N
C66 N
D88 N
A wire of cross-sectional area $3 m m^{2}$ is first stretched between two fixed points at a temperature of $20^{\circ} C$ . Determine the tension when the temperature falls to $10^{\circ} C$ Coefficient of linear expansion $α = 10^{- 5} .^{\circ} C^{- 1} and Y = 2 \times 10^{11} N / m^{2}$
A20 N
B30 N
C60 N
D120 N

Change in tension =T
$2 T {sin 37}^{\circ} - (Δ m) g$
$T = (Δ m) g$
$2 {sin 37}^{\circ}$
But $Δ l = \frac{T L}{A Y} = L \times (Δ θ)$
$\frac{(Δ m) g}{2 {sin 37}^{\circ}} \frac{1}{A Y} = α (Δ θ)$
$∴ Δ m = 12 k g$