Lines $L_{1}$ and $L_{2}$ have slopes m and n, respectively, suppose $L_{1}$ makes twice as large angle with the horizontal (mesured counter clockwise from the positive x-axis as does $L_{2}$ and $L_{1}$ has 4 times the slope of $L_{2}$ . If $L_{1}$ is not horizontal, then the value of the proudct mn equals.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2

Let $m = tan 2 θ$ and $n = tan θ$
And $m = 4 n$
and $m \neq 0$ .
$t h e r f or η n 2 θ \neq 0$
$∴ θ \neq 0$
$tan 2 θ = 4 tan θ$
$\Rightarrow \frac{2 tan θ}{1 - {tan}^{2} θ} = 4 tan θ$
$\Rightarrow 2 {tan}^{2} θ = 1$
$\Rightarrow {tan}^{2} θ = 1 / 2$
$\Rightarrow m n = tan 2 θ . tan θ$
$= \frac{2 {tan}^{2} θ}{1 - {tan}^{2} θ} = \frac{1}{1 - (/ 2)} = 2$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The eqautions of lines $L_{1} and L_{2}$ are $y = m x and y = n x$ , respectively. Suppose $L_{1}$ makes twice as large an angle with the horizontal (measured counterclockwise from the positive x - axis) as does $L_{2}$ and m = 4n, then the value of $\frac{(m^{2} + 4 n^{2})}{(m^{2} - 6 n^{2})}$ is equal to (where, $n \neq 0$ )
A3
B $- 3$
C2
D $- 2$
Question 2 - Select One
The area of triangle formed by the lines $l_{1} and l_{2}$ and the x-axis is:

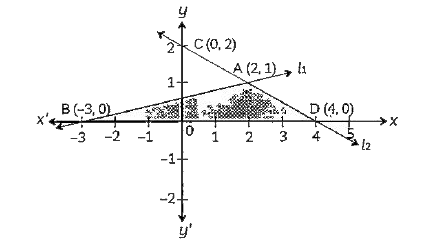A7 sq. units
B $\frac{9}{2}$ sq.units
C $\frac{7}{2}$ sq.units
D4 sq. units
Question 3 - Select One
In Fig., there are two convex lenses $L_{1} and L_{2}$ having focal lengths $F_{1}$ and $F_{2}$ respectively. The distance between $L_{1}$ and $L_{2}$ will be :
.
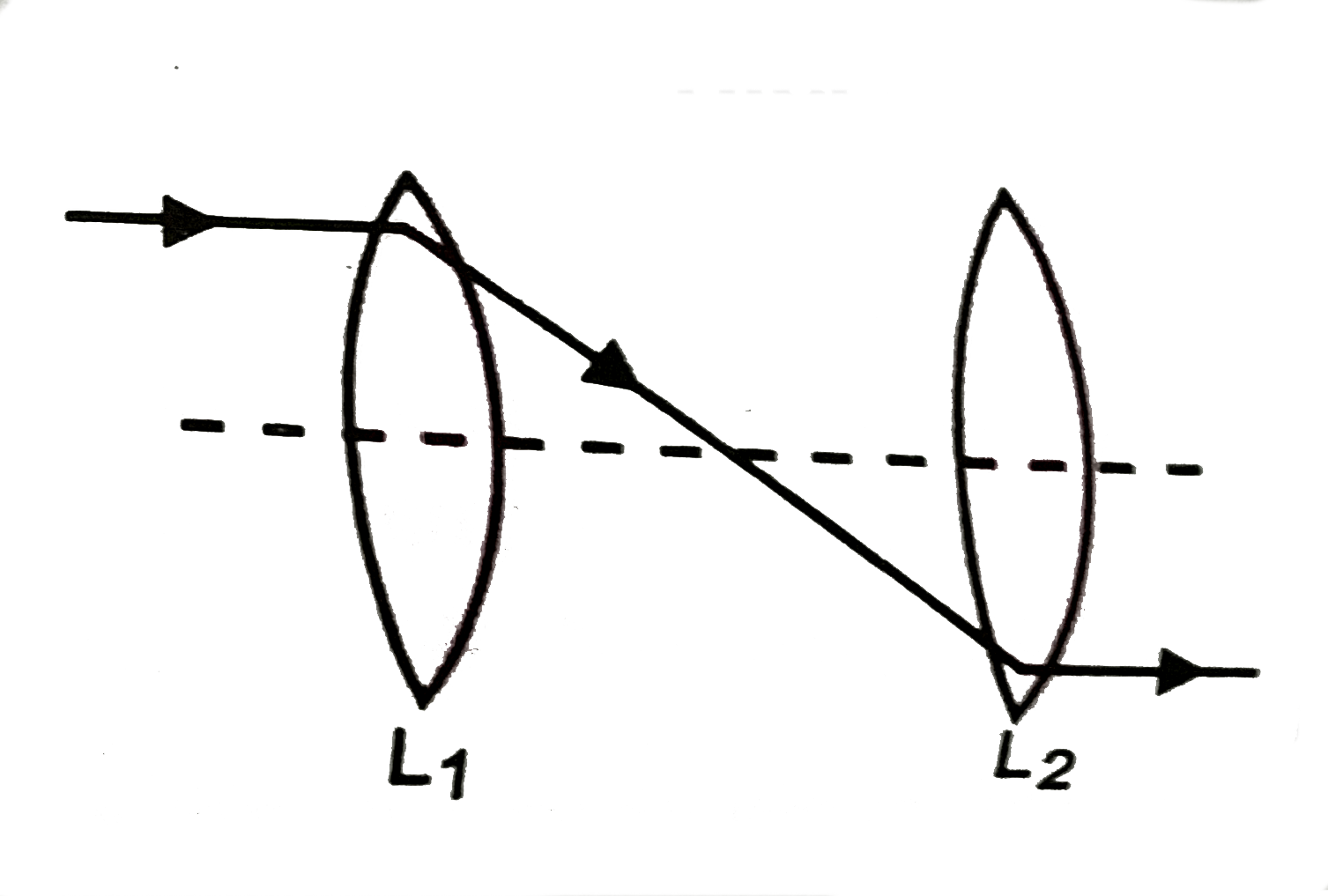A $F_{1}$
B $F_{2}$
C $F_{1} + f_{2}$
D $F_{1} - F_{2}$

CENGAGE-COORDINATE SYSYEM -Exercise (Numerical)

Home
Ask Doubt
Profile