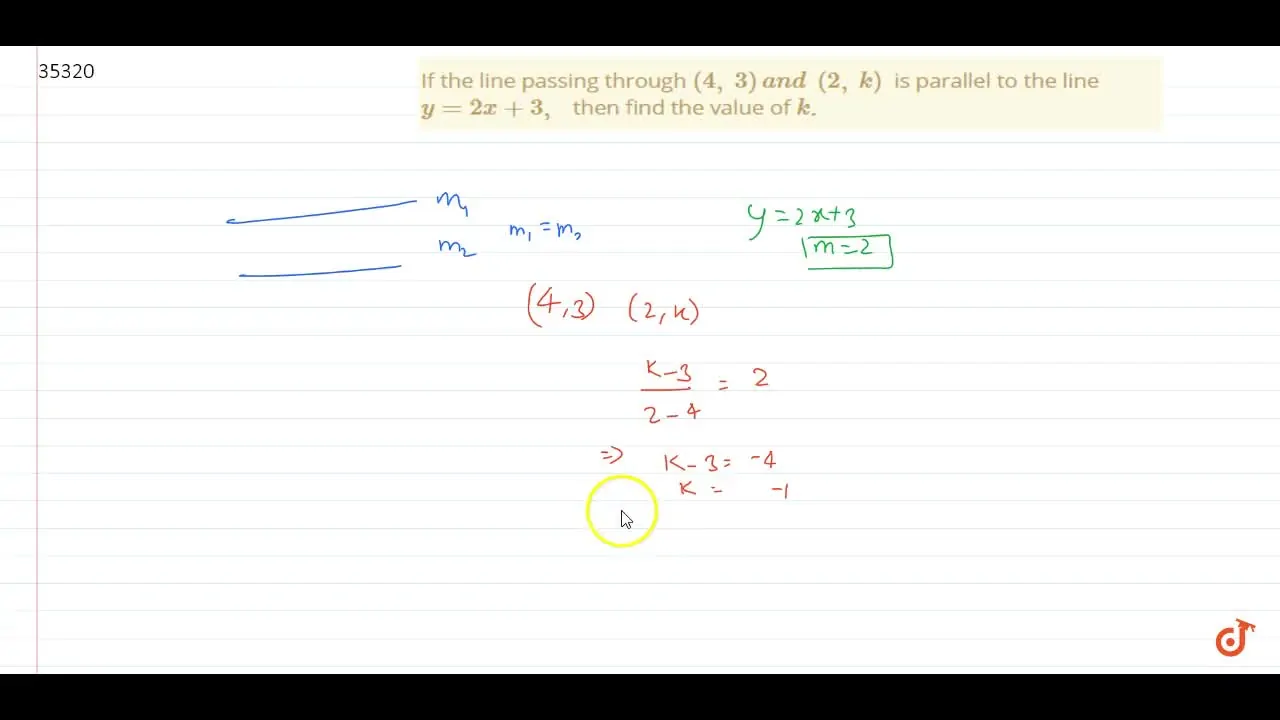
If the line passing through $(4, 3) a n d (2, k)$ is parallel to the line $y = 2 x + 3,$ then find the value of $k .$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $- 1$

The slope of line passing through (4,3) and (2,k)
$m_{1} = \frac{k - 3}{2 - 4} = \frac{3 - k}{2}$
The slope of the given line $y = 2 x + 3$ ,
$m_{2} = 2$
The lines are parallel. Therefore,
$\frac{3 - k}{2} = 2$
or $k = - 1$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Equation of the line passing through $(1, 2)$ and parallel to the line $y = 3 x - 1$ is
A $y + 2 = x + 1$
B $y + 2 = 3 (x + 1)$
C $y - 2 = 3 (x - 1)$
D $y - 2 = x - 1$
Question 2 - Select One
Equation of a line passing through (1,-2,3) and parallel to the plane $2 x + 3 y + z + 5 = 0$ is
A $\frac{x - 1}{- 1} = \frac{y + 2}{1} = \frac{z - 3}{- 1}$
B $\frac{x - 1}{2} = \frac{y + 2}{3} = \frac{z - 3}{1}$
C $\frac{x + 1}{- 1} = \frac{y - 2}{1} = \frac{z - 3}{- 1}$
Dnone of these

CENGAGE-COORDINATE SYSYEM -Exercise 1.4

Home
Ask Doubt
Profile