If the area enclosed by the curves $f (x) = {cos}^{- 1} (cos x) and g (x) = {sin}^{- 1} (cos x) in x \in [9 π / 4, 15 π / 4] is 9 π^{2} / b$ (where a and b are coprime), then the value of b is ____

Video Solution

Text Solution

Verified by Experts

The correct Answer is:8

We have $g (x) = {sin}^{- 1} (cos x) = \frac{π}{2} - {cos}^{- 1} (cos x)$
Both the curve bound the regions of same area in $[\frac{π}{4}, \frac{7 π}{4}], [\frac{9 π}{4}, \frac{15 π}{4}]$ and so on.

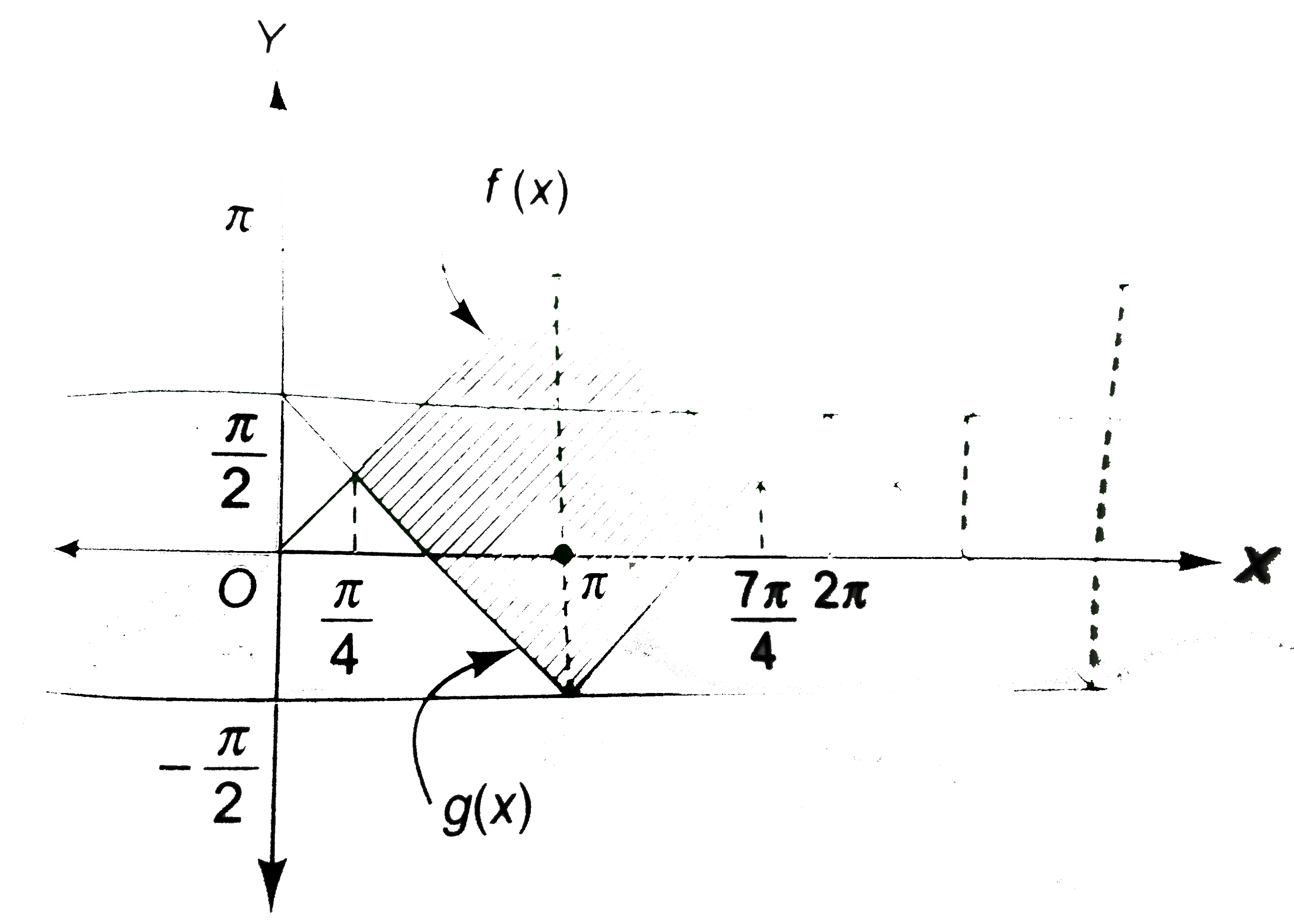
$∴$ Required area = Area of shaded square
$= \frac{9 π^{2}}{8} = \frac{a π^{2}}{b}$
$∴ a = 9 and b = 8$

|

Updated on:21/07/2023

Class 12 MATHS INVERSE TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area bounded by the curve $f (x) = {cos}^{- 1} (cos x), x \in [0, 2 π]$ with the tangent to the curve
$g (x) = | cos x | a t x = π,$ is
A ${(π + 1)}^{2}$ sq. units
B ${(π - 1)}^{2}$ sq. units
C $\frac{(π - 1) (2 π - 1)}{2}$ sq. units
Dnone of these
Question 2 - Select One
The value of ${sin}^{- 1} (cos (cos x) + {sin}^{- 1} (sin x)))$ where $x \in (\frac{π}{2}, π)$ is equal to
A $- π / 2$
B $π / 2$
C $- π$
D $π$
Question 3 - Select One
If $\begin{matrix} f (x) & = \frac{cos x - sin x}{cos 2 x} & , & x \neq \frac{π}{4} = k & , & x = \frac{π}{4} \end{matrix}$ is continous at $x = \frac{π}{4}$ , then the value of k is
A $\sqrt{2}$
B $\frac{1}{\sqrt{2}}$
C $2 \sqrt{2}$
D $\frac{1}{2 \sqrt{2}}$

CENGAGE-INVERSE TRIGONOMETRIC FUNCTIONS-Exercise (Numerical)

Home
Ask Doubt
Profile