Solver sin−1x>tan−1x
Video Solution
Text Solution
The correct Answer is:x∈(0,1)
We have sin−1x<tan−1x
Given inequality is meaningful if x∈[−1,1].
Now, let's draw the graph of y=sin−1xandy=tan−1x.
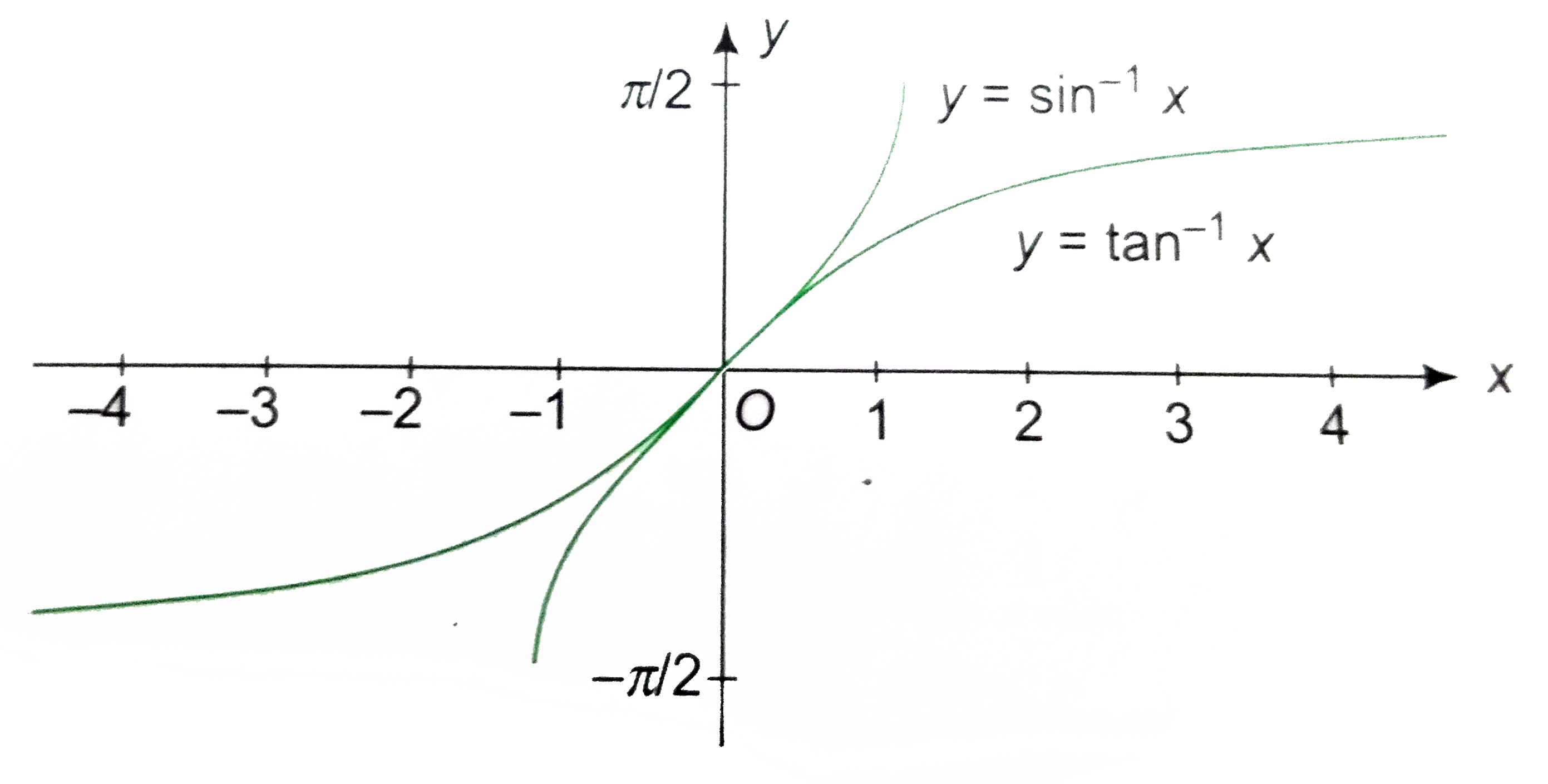
From the graph, we can see that sin−1x>tan−1x for x∈(0,1]
|
Topper's Solved these Questions
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.2
6 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.3
12 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Question Bank
24 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year
20 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
Similar Questions
Knowledge Check
Statement I sin−1(1√e)>tan−1(1√π)
Statement II sin−1x>tan−1y for x>y,∀x,y∈(0,1)AStatement I is True, Statement II is True, Statement II is a correct explanation for statement IBStatement I is True, Statement II is True, Statement II is NOT a correct explanation for Statement ICStatement I is True, Statement II is FalseDStatement I is False, Statement II is True.If cos−1x>sin−1x, then
A0≤x<1√2B−1<x<0Cx<0D−1≤x<1√2Let x1 and x2(x1>x2) be roots of the equation sin−1(cos(tan−1(cosec(cot−1x))))=π6, then
Asin−1.1x1+cos−1.1x2=πBsin−1(1x1)+cos−1(1x2)=0Csin−1.1x1+sin−1(1x2)=0Dcos−1(1x1)+cos−1(1x2)=π
