Let $a,$ $b$ and $c$ be three real numbers satisfying $[a, b, c] ⎡ ⎢ ⎣ \begin{matrix} 1 & 9 & 7 8 & 2 & 7 7 & 3 & 7 \end{matrix} ⎤ ⎥ ⎦ = [0, 0, 0]$ Let b=6, with a and c satisfying (E). If alpha and beta are the roots of the quadratic equation $a x^{2} + b x + c = 0$ then $\infty \sum n = 0 {(\frac{1}{α} + \frac{1}{β})}^{n}$ is

$\frac{6}{7}$

$\infty$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Let $b = 6$ with a and c satisfying (1). If $α$ and $β$ are the roots of the quadeatic equation $a x^{2} + b x + c = 0, t h e n$ is
A6
B7
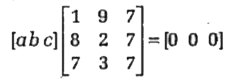C $\frac{6}{7}$
D $\infty$
If $α, β$ are the roots of the quadratic equation $a x^{2} + b x + c = 0 and 3 b^{2} = 16 a c$ , then
A $α = 4 β or β = 4 α$
B $α = - 4 β or β = - 4 α$
C $α = 3 β or β = 3 α$
D $α = - 3 β or β = - 3 α$
If $α$ and $β$ are the roots of the quadratic equation $x^{2} + b x - c = 0$ , then the equation whose roots are b and c, is
A $x^{2} + α x - β = 0$
B $x^{2} - [(α + β) + α β] x - α β (α - β) = 0$
C $x^{2} + [(α + β) + α β] x + α β (α + β) = 0$
D $x^{2} + [(α + β) + α β] x - α β (α + β) = 0$