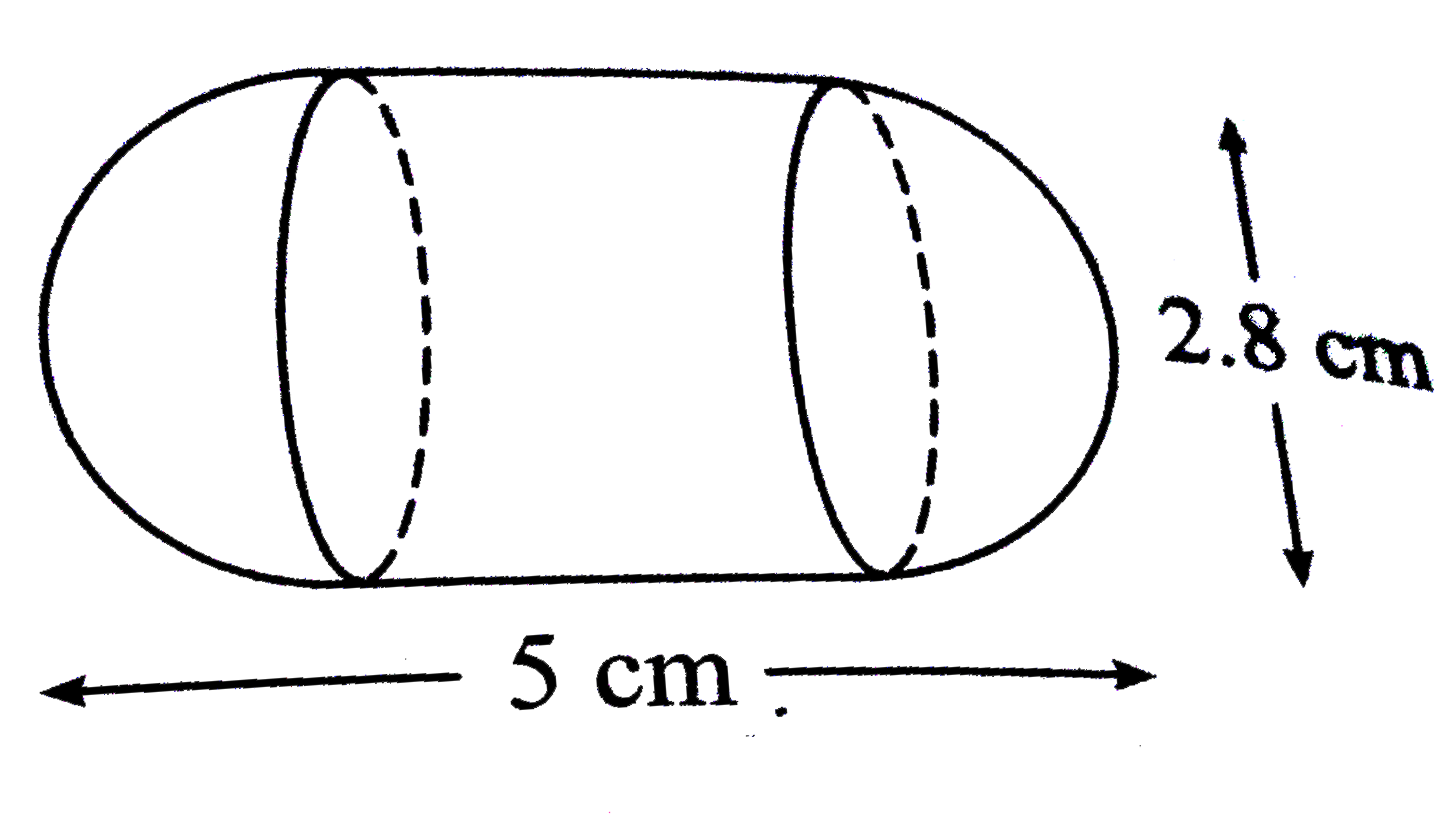
A gulab jamun, contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, eachshaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm
Total volume of gulab Jamun= volume of sphere+volume of cylinder
=43πr3+πr2h
=22⋅0.2⋅1.4⋅12.23
Total syrup of volume=30/100*volume of gulab jamun *tatal number of gulab jamun.
=310⋅22⋅.2⋅1.4⋅12.2⋅453
=338.184cm3
Similar Questions
A gulab jamun contains sugar syrup upto about 30% of its volume.
(1) Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm
(2) What mathematical concept is used in the above problem?
(Approximation type)
View SolutionA gulab jamun, contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, eachshaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm
View Solution
Knowledge Check
A medicine -capsule is the shape of a cylinder of diameter 0.5 cm with two hemisphere stuck to each of its ends. The length of entire capsule is 2cm. The capacity of the capsule is
A0.36cm3B0.35cm3C0.34cm3D0.33cm3
A gulabjamun when completely ready for eating contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulabjamuns shaped like a cylinder with two hemispherical ends, if the complete length of each of the gulabjamun is 5 cm and its diameter is 2.8 cm.
View SolutionA horizontally kept cylindrical vessel closed at both ends is separated into two equal (42 cm each) parts by an adiabatic piston. Both parts contain gas having equal mass at a temperature of 27∘C and a pressure of 1 atm. How much should the gas be heated in one part of the cylinder to shift the piston by 2 cm? Find the pressure p of the gas after shifting of the piston.
View SolutionThe lower end of a capillary tube of diameter 2.0 mm is dipped 8.00cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at temperature of the experiments is 7.30×10−2Nm−1. 1 atmospheric pressure =1.01×105Pa, density of water =1000kg/m3,g=9.80ms−2. also calculate the excess pressure.
View SolutionRachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
View SolutionShubham pal an engineering student was asket to make a model shaped like cylinder wih two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm .If each cone has a height of 32 cm , find the volufme of air contained i the model that shubham pal made. (Assume the outer and inner dimensions of the model to be nearly the same).
View SolutionThe lower end of a capillary tube of diameter 2.00 mm is dipped 8.00 cm below the surface of water in a beaker. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water? The surface tension of water at the temperature of the experiments is 7.30×10−2N/m. 1 atmospheric pressure =1.01×105Pa density of water =7000 kg/m3,g=9.80 ms−2. Also calculate the excess pressure.
View SolutionA circular ring of small thickness and of inner and outer diameters 3.8 cm and 4.2 cm respectively , suspended on one side of a common balance is exactly balanced by keeping sufficient mass in the pan on other side .At this instant the lower surface of ring is just resting on the surface of a liquid . Now if the ring is puled up gently , such that it does not loose its contact with the liquid , find how much mass should be changed in other pan , again to keep the balance in balanced position ? (Assume angle of contact is zero and surface tension of liquid is (1/π) N/m)
View Solution
