Let a, b and c be three real number satisfying
[a,b,c]∣∣
∣∣197827737∣∣
∣∣=[0,,0,0].....[E]
Let b=6, with a and c satisfying (E). If αandβ are the roots of the quadratic equation ax2+bx+c=0 then x∑n=0(1α+1β)n is
6
7
67
OO
The correct Answer is:B
Step by step video, text & image solution for Let a, b and c be three real number satisfying [a,b,c]|{:(,1,9,7),(,8,2,7),(,7,3,7):}|=[0,,0,0].....[E] Let b=6, with a and c satisfying (E). If alpha and beta are the roots of the quadratic equation ax^(2)+bx+c=0 then sum_(n=0)^(x) ((1)/(alpha)+(1)/(beta))^(n) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MATRICES & DETERMINANTBOOK - RESONANCECHAPTER - MATRICES & DETERMINANTEXERCISE - PART-II:
28 Videos
- MATRICES & DETERMINANTBOOK - RESONANCECHAPTER - MATRICES & DETERMINANTEXERCISE - HLP
33 Videos
- MATRICES & DETERMINANTBOOK - RESONANCECHAPTER - MATRICES & DETERMINANTEXERCISE - PART-IV
6 Videos
- INDEFINITE INTEGRATION BOOK - RESONANCECHAPTER - INDEFINITE INTEGRATION EXERCISE - SELF PRACTIC PROBLEMS
25 Videos
- NUMBER THEORYBOOK - RESONANCECHAPTER - NUMBER THEORYEXERCISE - Exercise -2 (PART - II)
4 Videos
Similar Questions
Let a,b, and c be three real numbers satistying [a,b,c]⎡⎢⎣197827737⎤⎥⎦=[0,0,0]Let b=6, with a and c satisfying (E). If alpha and beta are the roots of the quadratic equation ax2+bx+c=0then∞∑n=0(1α+1β)n is (A) 6 (B) 7 (C) 67 (D) oo
View SolutionLet b=6 ,with a and c satisfying the equation (a+b+c)2+(a+8b+7c)2=0. If α and β are the roots of the quadratic equation ax2+bx+c=0, then ∞∑n=0(1α+1β)n
View Solution
Knowledge Check
Let b=6 with a and c satisfying (1). If α and β are the roots of the quadeatic equation ax2+bx+c=0,then
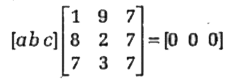 is A6B7C67D∞
is A6B7C67D∞If α,β are the roots of the quadratic equation ax2+bx+c=0and3b2=16ac, then
Aα=4βorβ=4αBα=−4βorβ=−4αCα=3βorβ=3αDα=−3βorβ=−3αTwo different real numbers αandβ are the roots of the quadratic equation ax2+c=0a,c≠0, then α3+β3 is:
AaB−cC0D−1
Let b=6 ,with a and c satisfying the equation (a+b+c)2+(a+8b+7c)2=0 .If α and β are the roots of the quadratic equation ax2+bx+c=0,then ∞∑n=0(1α+1β)n
View SolutionIf αandβ are the roots of the equation ax2+bx+c=0 , then an equation whose roots are 1αand1β is
View SolutionIf α,β are the roots of the quadratic equation x2+bx−c=0, the equation whose roots are b and c, is
View SolutionIf α and β are the roots of the equation 2x2+7x+c=0 and ∣∣α2−β2∣∣=74 then c=
View SolutionIf α and β are the roots of the quadratic equation x2+bx−c=0, then the equation whose roots are b and c, is
View Solution
