The coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0) respectively. The equation of the diagonal CE is:

A

√3x+y=4

B

x+√3y+4=0

C

x+√3y=4

D

none of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

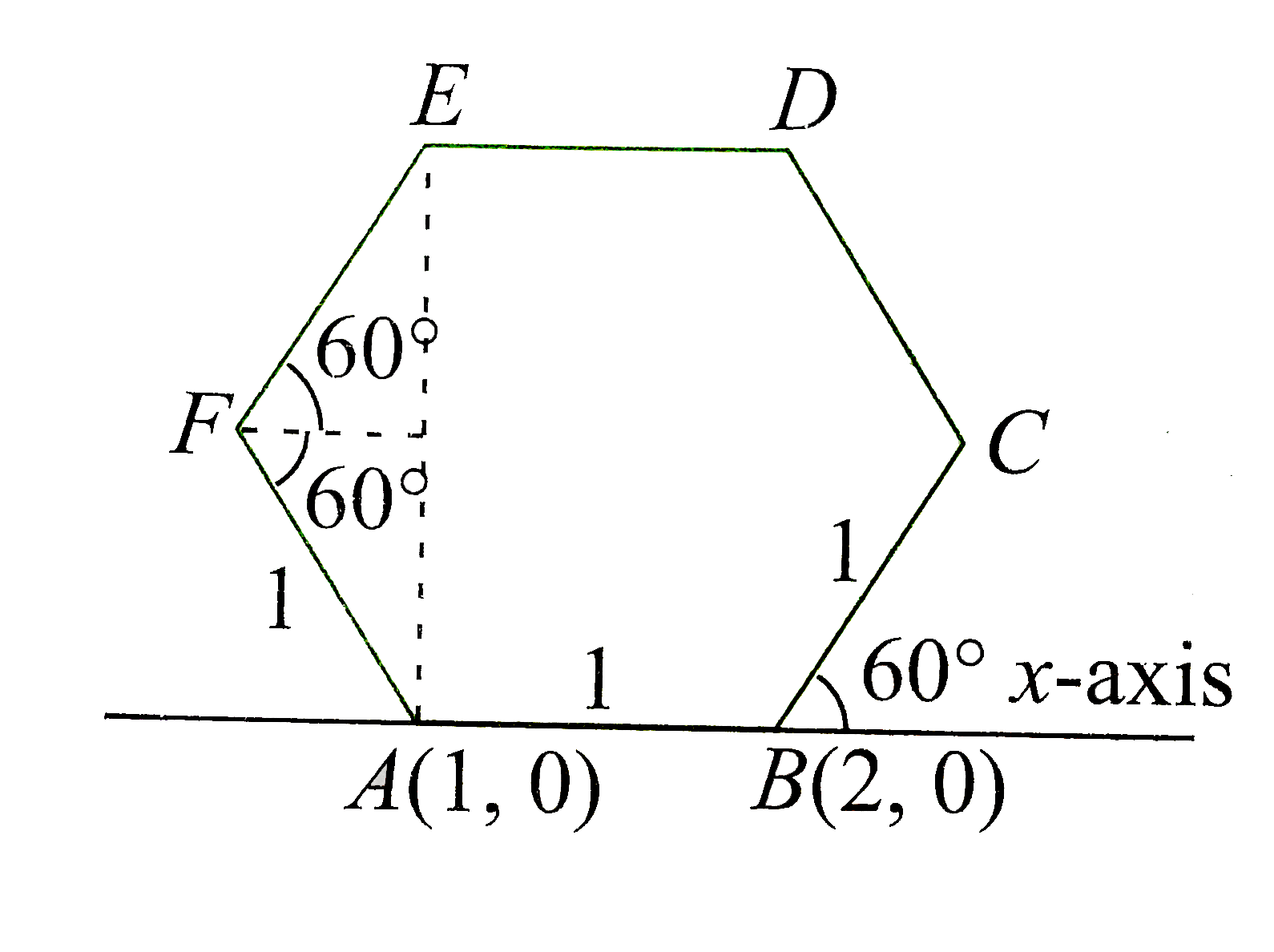
ocr_image
AB=1
or C≡(2+1×cos60∘,1×sin60∘)≡(52,√32)
E≡(1,1×sin60∘+1×sin60∘)≡(1,√3)
Therefore, the equation of CE is
y−√3=−1√3(x−1)

Updated on:21/07/2023
|
Class 12MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The coordinates of vertices A and B of an equilateral triangle ABC are (- 4, 0) and (4, 0) respectively. Which of the following could be coordinates of C

    A(0,2,√3)
    B(0,4)
    C(0,4qrt(3))
    D(0,3)

  • If ¯aand¯b represent the sides ¯¯¯¯¯¯ABand¯¯¯¯¯¯BC of a regular hexagon ABCDEF, then ¯¯¯¯¯¯FA=

    Ab−a
    Ba−b
    Ca+b
    Dnone of these