A rectangle PQRS has its side PQ parallel to the line $y = m x$ and vertices $P, Q$ , and $S$ on the lines $y = a, x = b$ ,and $x = - b$ , respectively. Find the locus of the vertex $R$ .

Video Solution

Text Solution

Verified by Experts

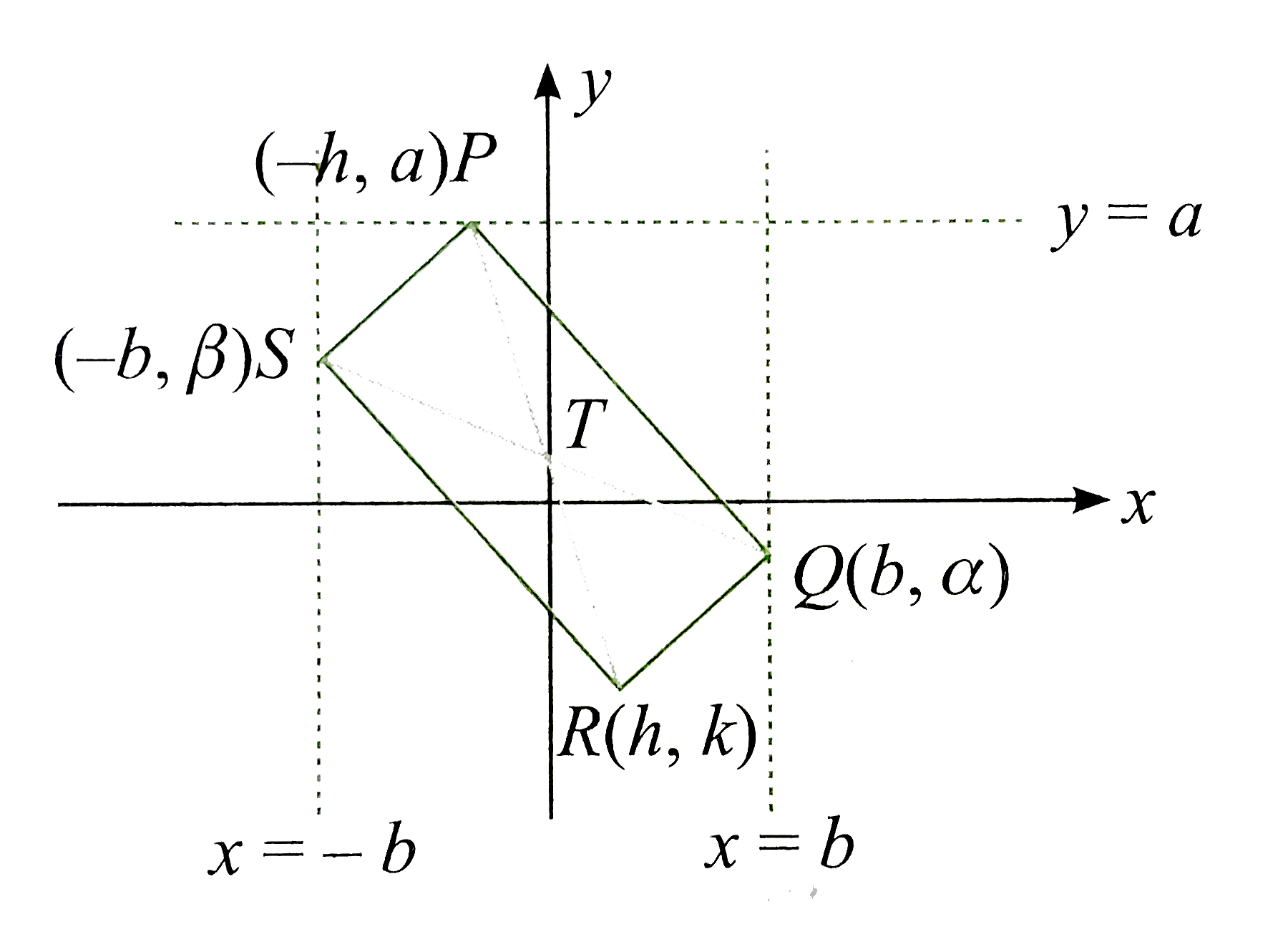
Let the coordinates of Q be $(b, α)$ and that of S be $(- b, β)$ .
Let PR and SQ intersect each other at T.
$∴ T is the mid point of SQ$
Since diagonal of a rectangle bisect each other, x co-ordinates of Pis -h.
As P lies on y=a, therefore coordinates of Pare (-h,a).
Given that PQ is parallel to y=mx and slope of PQ = m.
$∴ \frac{α - a}{b + h} = m$
$\Rightarrow α = a + m (b + h) (1)$
$Also, R Q ⊥ P Q \Rightarrow slope of R Q = \frac{- 1}{m}$
$∴ \frac{k - α}{h - b} = \frac{- 1}{m} \Rightarrow α = k + \frac{1}{m} (h - b) (2)$
From (1) and (2), we get
$a + m (b + h) = k + \frac{1}{m} (h - b)$
$\Rightarrow a m + m^{2} (b + h) = k m + (h - b)$
$\Rightarrow (m^{2} - 1) h - m k + b (m^{2} + 1) + a m = 0$
Therefore, locus of (h,k) is
$(m^{2} - 1) x - m y + b (m^{2} + 1) + a m = 0$

Updated on:21/07/2023

A rectangle ABCD has its side AB parallel to line y =x and vertices A,B and D lie on y = 1, x = 2 and x = -2, respectively. Locus of vertex 'C' is
Ax = 5
Bx-y = 5
Cy = 5
Dx+y = 5
A rectangle ABCD has its side AB parallel to line y =x and vertices A,B and D lie on y = 1, x = 2 and x = -2, respectively. Locus of vertex 'C' is
Ax = 5
Bx-y = 5
Cy = 5
Dx+y = 5
The image of P(a,b) in the line y=−x is Q and the image of Q in the line y=x is R. Then the midpoint of PR is
A $(a + b, b + a)$
B $((a + b) / 2, (b + 2) / 2)$
C $(a - b, b - a)$
D $(0, 0)$