Let a $\in$ R and f : $R \to R$ be given by $f (x) = x^{5} - 5 x + a$ , then
(a) $f (x) = 0$ has three real roots if $a > 4$
(b) $f (x) = 0$ has only one real root if $a > 4$
(c) $f (x) = 0$ has three real roots if $a < - 4$
(d) $f (x) = 0$ has three real roots if $- 4 < a < 4$

Video Solution

Text Solution

Verified by Experts

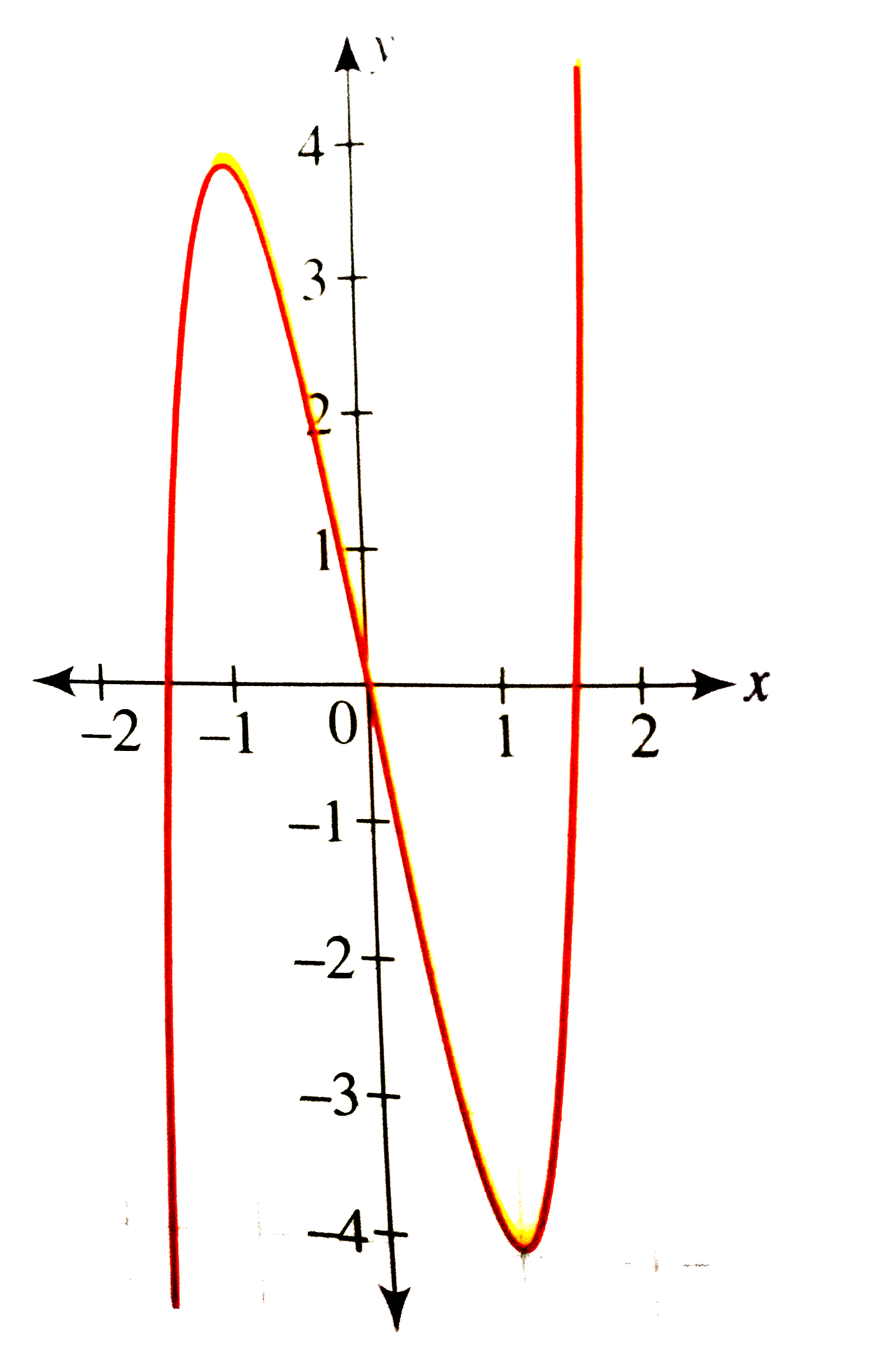
Let $= f (x) = x^{5} - 5 x$
$\Rightarrow f' (x) = 5 x^{4} - 5$
$= 5 (x^{4} - 1)$
$= 5 (x - 1) (x + 1) (x^{2} + 1)$
$f' (x) = 0, ∴ x = - 1, 1$
$f'' (x) = 20 x^{3}$
$f'' (1) = 20$ and $f'' (- 1) = - 20$
So x = 1 is the point of minima and x = -1 is the point of maxima.
Also $f (1) = - 4$ and $f (- 1) = 4$
Graph of $y = f (x)$ is as shown in the adjacent figure.
From the graph, $x^{5} - 5 x = - a$ has one real root if $- a < - 4$ or $- a > 4$ ,
i.e. $a > 4$ or $a < - 4$
Also $x^{5} - 5 x = - a$ has three real roots if $- 4 < - a < 4$
i.e. $- 4 < a < 4$
Hence correct answers are (b) and (d).

Updated on:21/07/2023

If the equaion $x^{2} + a x + b = 0$ has distinct real roots and $x^{2} + a | x | + b = 0$ has only one real root, then
A $b = 0, a > 0$
B $b = 0, a < 0$
C $b > 0, a < 0$
D $b < 0, a > 0$
For what value of a, does the function $f (x) = x^{5} - 5 x + a$ has three real roots ?
A $a > 4$
B $a < 4$
C $- 4 < a < 4$
D $- 4 \leq a \leq 4$