Sketch the graph of the following functions $y = f (x)$ and find the number of real roots of the corresponding equation $f (x) = 0$ .
$(i) f (x) = 2 x^{3} - 9 x^{2} + 12 x - (9 / 2) (i i) f (x) = 2 x^{3} - 9 x^{2} + 12 x - 3$

Video Solution

Text Solution

Verified by Experts

(i) We have $y = f (x) = 2 x^{3} - 9 x^{2} + 12 x - (9 / 2)$
$∴ f' (x) = 6 x^{2} - 18 x + 12 = 6 (x^{2} - 3 x + 2) = 6 (x - 1) (x - 2)$
Now $f' (x) = 0 \Rightarrow x = 1 and x = 2$
The sign scheme of $y = f' (x)$ is as follows.

So $x = 2$ is the point of minima and $x = 1$ is the point of maxima.
$f (1) = 2 - 9 + 12 - (9 / 2) > 0$
and $f (2) = 16 - 36 + 24 - (9 / 2) < 0$
Hence the graph of the function $y = f (x)$ is as shown in the following figure.

As shown in the figure, the graph cute the x-axis at three distinct points.
Hence the equation $f (x) = 0$ has three distinct roots.
(ii) We have $y = f (x) = 2 x^{3} - 9 x^{2} + 12 x - 3$
$f' (x) = 0 \Rightarrow x = 1$ and $x = 2$
Also $f (1) = 2 - 9 + 12 - 3 = 2 and f (2) = 16 - 36 + 24 - 3 = 1$
Hence the graph of $y = f (x)$ is as shown in the following figure.

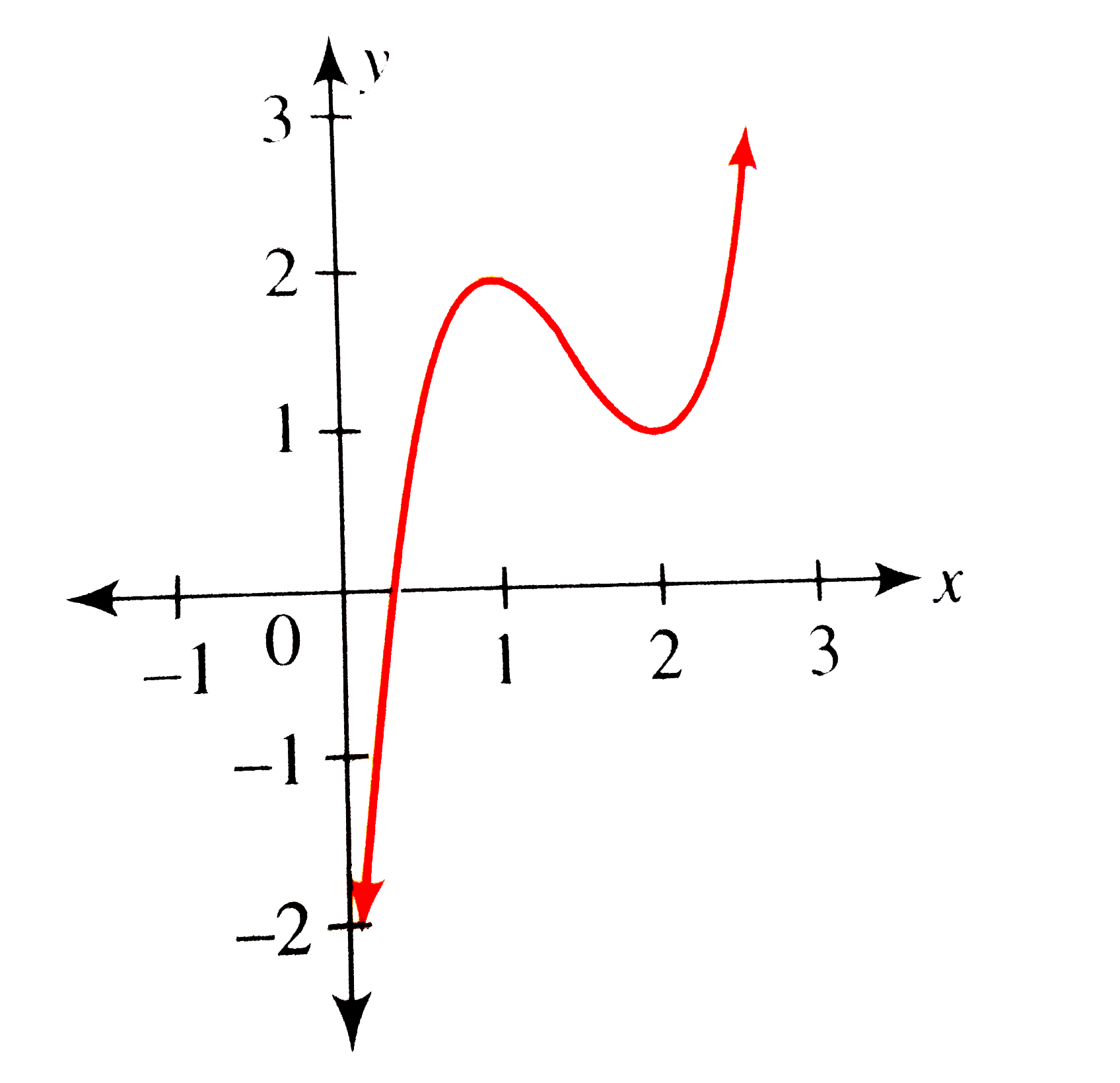
Thus, from the graph we can see that $f (x) = 0$ has only one real root, though $y = f (x)$ has two turning points.

Updated on:21/07/2023

If $f (x) = x^{3} - 9 x^{2} + 24 x,$ then f
Ahas maximum value =36
Bhas minimum value =16
Chas minima at x=2
Dhas maxima at x=4
If $f (x) = x^{3} - 9 x^{2} + 24 x,$ then f
Ahas maximum value =16
Bhas minimum value =10
Chas minima at x=2
Dhas maxima at x=2
Maximum value of $f (x) = 2 x^{3} - 9 x^{2} + 12 x - 2$ is
A $1$
B $2$
C $3$
D $4$