Question

Draw the rough sketch of the curve $y={(x-1)}^2(x-2){(x-3)}^3$.

Explanation

We have `y=f(x)=(x-1)^(2)(x-2)(x-3)^(3)`
The sign scheme of `y=f(x)` is as follows.

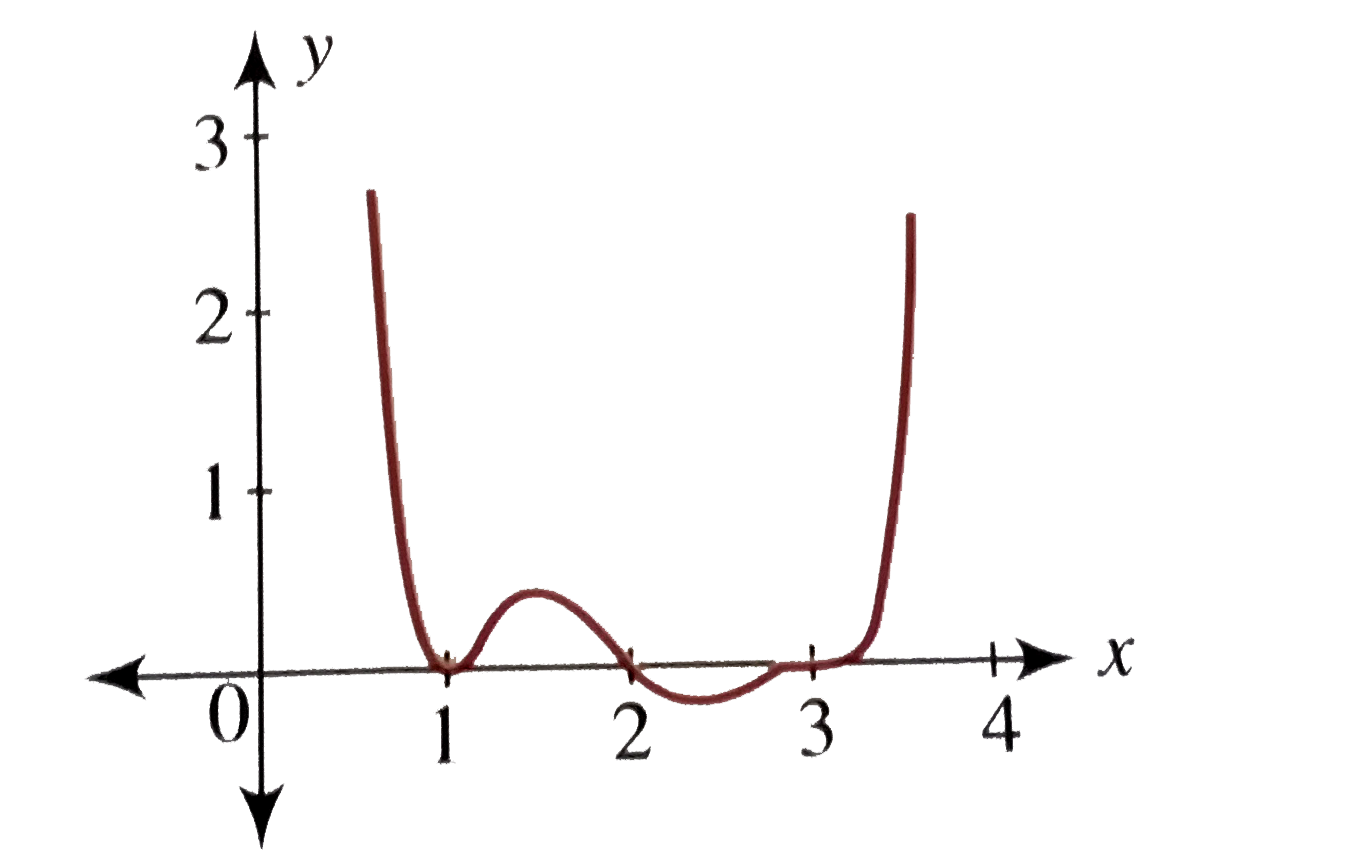
`(x-3)^(3)rarr` Curve crosses the x-axis at (3,0) and also touches the x-axis.
`(x-2)rarr` Curve crosses the x-axis at (2,0) without touching the x-axis.
`(x-1)^(2) rarr` Curve does not cross the x-axis but touches the x-axis at (1,0).
Hence the rough sketch of the curve `y=f(x)` is as shown in the following figure.