J.C. Slater proposed an empirical constant that represents the cumulative extent to which the other electrons of an atom shield (or screen) any particular electron from the nuclear charge. Thus, slater's screening contant σ is as : Z∗=Z−σ
Here, Z is the atomic number of the atom, and hence is equal to the actual number of protons in the atom. the parameter Z∗ is the effective nuclear charge, which according to is smaller than Z, since the electron in question is screened (shielded) from Z by an amount σ. Conversely, an electron that is well shielded from the nuclear charge Z experiences a small effective nuclear charge Z∗.
The value of σ for any one electron in a given electron configuration (i.e., in the presence of the other electrons of the atom in question) is calculated using a set of empirical rules developed by slater. according to these rules, the value of σ for the electron in question is the cumulative total provided by the various other electrons of the atom.
Q. According to Slater's rule, order of effective nuclear charge (Z∗) for last electron in case of Li, Na and K.
Li>Na>K
K>Na>Li
Na>Li>K
K=Na>Li
The correct Answer is:D
3Li⇒3−(0.85×2)⇒1.3
11Na⇒11−(0.85×8+1×2)=11−8.8=2.2
19K⇒19−(0.85×8+1×10)=19−16.8=2.2
Topper's Solved these Questions
- PERIODIC PROPERTIESBook:VK JAISWALChapter:PERIODIC PROPERTIESExercise:ONE OR MORE ANSWERS IN/ARE CORRECT
Explore 99 Videos
- PERIODIC PROPERTIESBook:VK JAISWALChapter:PERIODIC PROPERTIESExercise:MATCHTHE COLUMN
Explore 5 Videos
- p-BLOCK ELEMENTSBook:VK JAISWALChapter:p-BLOCK ELEMENTSExercise:SUBJECTIVE PROBLEMS
Explore 36 Videos
- QUALITATIVE INORGANIC ANALYSISBook:VK JAISWALChapter:QUALITATIVE INORGANIC ANALYSISExercise:SUBJECTIVE PROBLEMS
Explore 5 Videos
Similar Questions
Assign the position of the element having outer electronic configuration,
(A) ns2np2 (n=6)
(B) (n−1)d2ns2 (n=4)
(C) (n−2)f7(n−1)d−1ns2 (n=6)
Which of the following statement(s) is/are correct?
View Solution
View SolutionIn phosphorus acid, If X is number of non-bonding electron pairs. Y is number of σ-bonds and Z is number of π-bonds. Then calculate value of "YxZ-X".
View SolutionConsider the following reaction
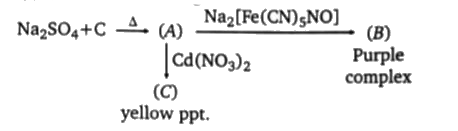
Then calculate value of ∣∣X2−Y2∣∣ (where X and Y are total number of electrons present t_(2g) and e_(g) orbitals respectively in d-block metal ion of compound B).
View SolutionAccording to I.C slater effective nuclear charge, Z∗, due to screening, is not exactly equal to the actual nuclear charge Z of the nucleus of the atom. Z∗ depends on the type of orbitals in which the electron is housed, and on the ability of other electrons in more penetrating orbitals to screen the electron in question from the nucleus.
The relative extent to which the various orbitals penetrate the electron clouds of other orbitals is s>p>f . The effective nuclear charge Z∗ due to screening is given by Z∗=Z−σ, where Z is the atomic atomic number and σ is the slater screening constant values 0<σ<Z

Screening effect of one electron in the outermost orbitals, is not considered in calculate of σ.
What is the value of Z∗ for Rb(37) ?
View SolutionAccording to I.C slater effective nuclear charge, Z∗, due to screening, is not exactly equal to the actual nuclear charge Z of the nucleus of the atom. Z∗ depends on the type of orbitals in which the electron is housed, and on the ability of other electrons in more penetrating orbitals to screen the electron in question from the nucleus.
The relative extent to which the various orbitals penetrate the electron clouds of other orbitals is s>p>f . The effective nuclear charge Z∗ due to screening is given by Z∗=Z−σ, where Z is the atomic atomic number and σ is the slater screening constant values 0<σ<Z

Screening effect of one electron in the outermost orbitals, is not considered in calculate of σ.
what is Z∗ for Cu(29) ?
View SolutionAccording to I.C slater effective nuclear charge, Z^(**) , due to screening, is not exactly equal to the actual nuclear charge Z of the nucleus of the atom. Z^(**) depends on the type of orbitals in which the electron is housed, and on the ability of other electrons in more penetrating orbitals to screen the electron in question from the nucleus. The relative extent to which the various orbitals penetrate the electron clouds of other orbitals is s gt p gt f . The effective nuclear charge Z^(**) due to screening is given by Z^(**)=Z-sigma , where Z is the atomic atomic number and sigma is the slater screening constant values 0 lt sigma lt Z Screening effect of one electron in the outermost orbitals, is not considered in calculate of sigma . What is the value of Z^(**) for Rb(37) ?
View SolutionAccording to I.C slater effective nuclear charge, Z∗, due to screening, is not exactly equal to the actual nuclear charge Z of the nucleus of the atom. Z∗ depends on the type of orbitals in which the electron is housed, and on the ability of other electrons in more penetrating orbitals to screen the electron in question from the nucleus.
The relative extent to which the various orbitals penetrate the electron clouds of other orbitals is s>p>f . The effective nuclear charge Z∗ due to screening is given by Z∗=Z−σ, where Z is the atomic atomic number and σ is the slater screening constant values 0<σ<Z

Screening effect of one electron in the outermost orbitals, is not considered in calculate of σ.
In which of the following cases the concept of Z∗ is applicable?
View SolutionThe reducing effect of the nuclear charge by the inner electrons for on outer electron is termed aas shielding (or screening). As a result of shielding, the outer electrons in an atom always experience less nnuclear charge than the actual nuclear charge Z. The effective nuclear charge (Z∗) as experienced by an electron is then obtained by subtracting the total shielding contributions from alll the other electrons (i.e., except the one under consideration) from the actual nuclear charge.
Z∗=Z−σ
Where σ=sum of the shielding contributions. The rules for estimating contributions to σ are as follows (Slater's rule) Contribution to shielding by each electron is :
∣∣ ∣ ∣ ∣ ∣ ∣∣ElectronAll HigherSameGroupGroup≤GrpoupGroupGroupn−1n−21s 00.30−−(ns,sp) 00.350.851.00(nd)or(nf) 00.351.001.00∣∣ ∣ ∣ ∣ ∣ ∣∣
According to Slater's treatment, the energy of an electron in nth shell of an atom having atomic number Z is given by the empirical equation
E=−13.6(Z∗n)2eV
Z∗ = effective nuclear charge
Among the following, which electron of Fe atom experience minimum attraction from nucleus? (Atomic number of Fe=26)
View SolutionThe reducing effect of the nuclear charge by the inner electrons for on outer electron is termed aas shielding (or screening). As a result of shielding, the outer electrons in an atom always experience less nnuclear charge than the actual nuclear charge Z. The effective nuclear charge (Z^(**)) as experienced by an electron is then obtained by subtracting the total shielding contributions from alll the other electrons (i.e., except the one under consideration) from the actual nuclear charge. Z^(**)=Z-sigma Where sigma =sum of the shielding contributions. The rules for estimating contributions to sigma are as follows (Slater's rule) Contribution to shielding by each electron is : |{:("Electron","All Higher","Same","Group","Group"le),("Grpoup","Group","Group",n-1,n-2),(1s," "0,0.30,-,-),((ns,sp)," "0,0.35,0.85,1.00),((nd)or(nf)," "0,0.35,1.00,1.00):}| According to Slater's treatment, the energy of an electron in nth shell of an atom having atomic number Z is given by the empirical equation E=-13.6((Z^(**))/(n))^(2)eV Z^(**) = effective nuclear charge Z^(**) for a 1st electron in Fe atom is:
View SolutionThe reducing effect of the nuclear charge by the inner electrons for on outer electron is termed aas shielding (or screening). As a result of shielding, the outer electrons in an atom always experience less nnuclear charge than the actual nuclear charge Z. The effective nuclear charge (Z^(**)) as experienced by an electron is then obtained by subtracting the total shielding contributions from alll the other electrons (i.e., except the one under consideration) from the actual nuclear charge. Z^(**)=Z-sigma Where sigma =sum of the shielding contributions. The rules for estimating contributions to sigma are as follows (Slater's rule) Contribution to shielding by each electron is : |{:("Electron","All Higher","Same","Group","Group"le),("Grpoup","Group","Group",n-1,n-2),(1s," "0,0.30,-,-),((ns,sp)," "0,0.35,0.85,1.00),((nd)or(nf)," "0,0.35,1.00,1.00):}| According to Slater's treatment, the energy of an electron in nth shell of an atom having atomic number Z is given by the empirical equation E=-13.6((Z^(**))/(n))^(2)eV Z^(**) = effective nuclear charge Atomic radii of the noble gases are larger than the precedent elements of the same periods because:
View SolutionThe reducing effect of the nuclear charge by the inner electrons for on outer electron is termed aas shielding (or screening). As a result of shielding, the outer electrons in an atom always experience less nnuclear charge than the actual nuclear charge Z. The effective nuclear charge (Z^(**)) as experienced by an electron is then obtained by subtracting the total shielding contributions from alll the other electrons (i.e., except the one under consideration) from the actual nuclear charge. Z^(**)=Z-sigma Where sigma =sum of the shielding contributions. The rules for estimating contributions to sigma are as follows (Slater's rule) Contribution to shielding by each electron is : |{:("Electron","All Higher","Same","Group","Group"le),("Grpoup","Group","Group",n-1,n-2),(1s," "0,0.30,-,-),((ns,sp)," "0,0.35,0.85,1.00),((nd)or(nf)," "0,0.35,1.00,1.00):}| According to Slater's treatment, the energy of an electron in nth shell of an atom having atomic number Z is given by the empirical equation E=-13.6((Z^(**))/(n))^(2)eV Z^(**) = effective nuclear charge Which of the following statements is correct?
View SolutionThe reducing effect of the nuclear charge by the inner electrons for on outer electron is termed aas shielding (or screening). As a result of shielding, the outer electrons in an atom always experience less nnuclear charge than the actual nuclear charge Z. The effective nuclear charge (Z^(**)) as experienced by an electron is then obtained by subtracting the total shielding contributions from alll the other electrons (i.e., except the one under consideration) from the actual nuclear charge. Z^(**)=Z-sigma Where sigma =sum of the shielding contributions. The rules for estimating contributions to sigma are as follows (Slater's rule) Contribution to shielding by each electron is : |{:("Electron","All Higher","Same","Group","Group"le),("Grpoup","Group","Group",n-1,n-2),(1s," "0,0.30,-,-),((ns,sp)," "0,0.35,0.85,1.00),((nd)or(nf)," "0,0.35,1.00,1.00):}| According to Slater's treatment, the energy of an electron in nth shell of an atom having atomic number Z is given by the empirical equation E=-13.6((Z^(**))/(n))^(2)eV Z^(**) = effective nuclear charge Which one among the following sets of ions represents the collection of isoelectronic species?
View SolutionTell the relation between effective nuclear charge (Zeff) atomic number (Z) and shielding constant (σ). Explain it qualitatively.
View SolutionJ.C. Slater proposed an empirical constant that represents the cumulative extent to which the other electrons of an atom shield (or screen) any particular electron from the nuclear charge. Thus, slater's screening contant sigma is as : Z^(**)=Z-sigma Here, Z is the atomic number of the atom, and hence is equal to the actual number of protons in the atom. the parameter Z^(**) is the effective nuclear charge, which according to is smaller than Z, since the electron in question is screened (shielded) from Z by an amount sigma . Conversely, an electron that is well shielded from the nuclear charge Z experiences a small effective nuclear charge Z^(**) . The value of sigma for any one electron in a given electron configuration (i.e., in the presence of the other electrons of the atom in question) is calculated using a set of empirical rules developed by slater. according to these rules, the value of sigma for the electron in question is the cumulative total provided by the various other electrons of the atom. Q. The effective nuclear charge at the periphery of chromium atom [Z=24]:
View Solution

