A cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
1/n
1n+1
nn=1
n+1n
The correct Answer is:C
To find the ratio of the terminal potential difference (V) to the electromotive force (E) of a cell connected in series with an external resistance, we can follow these steps:
1. Identify the Components:
- Let the EMF of the cell be E.
- Let the internal resistance of the cell be r.
- Let the external resistance be nr, where n is a constant.
2. Calculate the Total Resistance:
- The total resistance Rtotal in the circuit is the sum of the internal resistance and the external resistance:
Rtotal=r+nr=r(1+n)
3. Determine the Current in the Circuit:
- Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=ERtotal=Er(1+n)
4. Calculate the Terminal Potential Difference (V):
- The terminal potential difference V can be expressed using the formula:
V=E−I⋅r
- Substituting the value of I:
V=E−(Er(1+n))⋅r
- Simplifying this:
V=E−E1+n
- To combine these terms, we can find a common denominator:
V=E(1+n)−E1+n=En1+n
5. Find the Ratio of Terminal Potential Difference to EMF:
- Now, we need to find the ratio VE:
VE=En1+nE
- This simplifies to:
VE=n1+n
Final Answer:
The ratio of the terminal potential difference to the EMF is:
VE=nn+1
- Let the EMF of the cell be E.
- Let the internal resistance of the cell be r.
- Let the external resistance be nr, where n is a constant.
- The total resistance Rtotal in the circuit is the sum of the internal resistance and the external resistance:
Rtotal=r+nr=r(1+n)
- Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=ERtotal=Er(1+n)
- The terminal potential difference V can be expressed using the formula:
V=E−I⋅r
- Substituting the value of I:
V=E−(Er(1+n))⋅r
- Simplifying this:
V=E−E1+n
- To combine these terms, we can find a common denominator:
V=E(1+n)−E1+n=En1+n
- Now, we need to find the ratio VE:
VE=En1+nE
- This simplifies to:
VE=n1+n
The ratio of the terminal potential difference to the EMF is:
VE=nn+1
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:ASSIGNMENT PROBLEMS (OBJECTIVE)(Level-II)
Explore 20 Videos
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:Comprehension -(1)
Explore 5 Videos
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE)(Level-II//III)
Explore 14 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:(NUMERICAL BASED QUESTIONS)
Explore 4 Videos
- ELASTICITY AND WAVES Book:FIITJEEChapter:ELASTICITY AND WAVES Exercise:Assignment Problems (Objective) Level-II
Explore 15 Videos
Similar Questions
A cell of emf E and internal resistance r is connected in series with an external resistance nr. Than what will be the ratio of the terminal potential difference to emf, if n=9.
View SolutionA cell of emf ε and internal resistance (r) is connected in series with an external resistance (nr) then the ratio of the terminal potential difference to emf is:
View Solution
Knowledge Check
A cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
A(1n)B1(n+1)Cn(n+1)D(n+1)nA cell of e.m.f (E) and internal resistance (r) is connected in series with an external resistance (nr.) then the ratio of the terminal p.d. to E.M.F is
A1/nB1/(n+1)Cn/(n+1)D(n+1)/nA cell of emf (E) and internal resistance r is connected across a variable external resistance . R. The graph of terminal potential difference V as a function of R is
A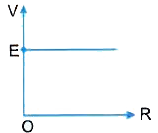 B
B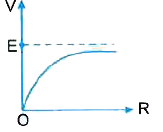 C
C D
D
A circuit consists of two cells, each of e.m.f. E and internal resistances r1 and r2 are connected in series through an external resistance X. If the potential difference between the ends of the first cell is zero, the value of X in terms of r1 and r2 will be
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance reverse. Then, the current in the external circuit is
View SolutionTow cells with the same emf E and different internal resistances r1 and r2 are connected in series to an external resistances R . The value of R so that the potential difference across the first cell be zero is
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionThere are n cells, each of emf E and internal resistance r, connected in series with an external resistance R. One of the cells is wrongly connected, so that it sends current in the opposite direction. The current flowing in the circuit is
View Solution